Um artigo em Tappi (1960, Vol.43, pp. 38-44) descreve um experimento que investigou o valor da cinza da polpa de papel (uma medida de impurezas inorgânicas). Duas variáveis, temperatura , em graus Celsius, e tempo, em horas, foram estudadas, sendo alguns resultados mostrados na tabela seguinte. As variáveis preditoras codificadas mostradas são
,
E a resposta é (valor da cinza seca em %) .
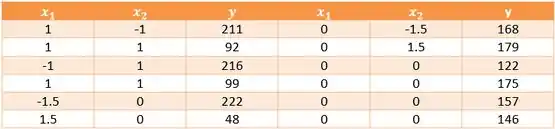
Que tipo de planejamento foi usado nesse estudo? Esse planejamento é rotacionável?
Ajuste um modelo quadrático aos dados. Esse modelo é satisfatório?
Se for importante minimizar o valor da cinza, onde correria o processo?
Passo 1
Bom galera, vamos começar traçancos os pontos em que os experimento foram feitos, fica assim:
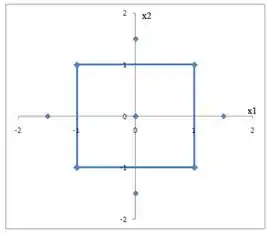
Assim vemos que há pontos de um planejamento fatorial , 4 execuções axiais e 5 execuções no centro do ponto. Isso é um planejamento composto cetral e não é rotacionável.
Passo 2
Beleza, agora a gente considera o modelo para observações e na notação matricial. Para obtermos o modelo de regressão que funcione precisamos usar a formula:
O vetor dos resíduos é dado por: .
O estimador da variante é .
A regressão da soma dos quadrados é:
O coeficiente de determinação múltipla é .
Então nós chegamos no modelo:
Passo 3
Show de bola, usando o Minitab para encontrar a equação de regressão. Nós encontraremos:
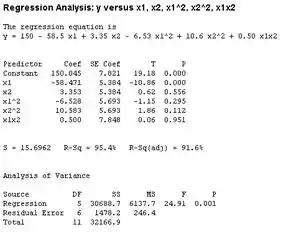
E com isso temos:
Passo 4
Agora, vamos aos valores de dos t-testes para testar hipóteses nulas de para quando a constante e o termo linear forem pequenos, logo podemos concluir que esses termos são significativos. Mas em nós não podemos concluir qu os termos da regressão são significativos. Portanto o modelo não é satisfatório.
Passo 5
Por fim, vamos plotar superfície formada:
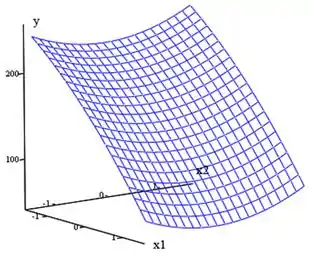
Observando a gente nota que o valor mínimo para é obtido quando , .
Resposta
Isso é um planejamento composto cetral e não é rotacionável.
Os termos lineares são significativos, enquanto os termos quadráticos e os termos de interação não são significativos.
O valor mínimo para é obtido quando , .