Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 11.Exercícios - Ex. 35

O artigo "Variation in Moisture and Ascorbic Acid Content from Leaf to Leaf and Plant to Plant in Tumip Greens" (Southern Cooperative Services Bull., 1951, p. 13-17) emprega um modelo em quadrado latino em que o fator A é uma planta, o fator B é o tamanho da folha (da menor a maior), o fator C (entre parênteses) é o tempo de pesagem e a variável de resposta ê a quantidade de umidade.

Quando os três fatores são aleatórios, os quadrados médios esperados sāo E ( Q M A ) = σ 2 + N σ A 2 , E ( Q M B ) = σ 2 + N σ त   2 , E ( Q M C ) = σ 2 + N σ C 2 e E ( Q M E ) = σ 2 . Isso significa que as razōes F para testar H O A : σ A 2 = 0 , H O x : σ D ‾ 2 = 0 e H 0 c : σ c 2 = 0 são idênticas à razōes para efeitos fixos. Obtenha a tabela ANOVA e teste para verificar se, ao nível 0,05 , há alguma variaçāo na quantidade de umidade decorrente dos fatores.

Passo 1

Obtenha a tabela ANOVA e teste para verificar se, ao nível 0,05 , há alguma variaçāo na quantidade de umidade decorrente dos fatores.

x = 180.09 , C F = 1297.30 , Σ Σ x i j ( k ) 2 = 1358.60

F 4,12 = 3,26 ,   então tanto o fator A (planta) quanto o B (tamanho da folha) parecem afetar o teor de umidade, mas o fator C (tempo de pesagem) não.

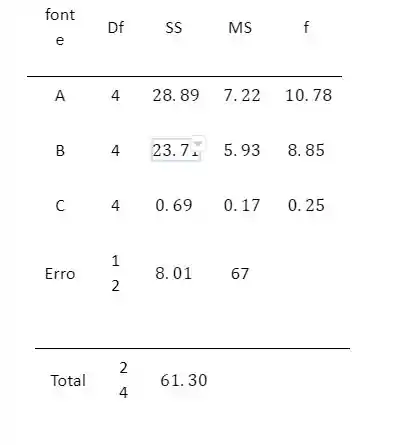
Resposta

F 4,12 = 3,26 ,   então tanto o fator A (planta) quanto o B (tamanho da folha) parecem afetar o teor de umidade, mas o fator C (tempo de pesagem) não.

Exercícios de Livros Relacionados

a. Em um experimento de sete fatores ( A , … , G ) , suponha que uma replicação pelo quarto seja de fato realizada. Se os efeitos determinantes forem A B C D E e C D E F G , qual será o terceiro efeit
Uma replicação pela metade de um experimento 2 5 para investigar os efeitos do tempo de aquecimento ( A ) , do tempo de esfriamento ( B ) , do tempo de trefilação ( C ) , da posição das serpentinas de
Um experimento realizado para investigar os efeitos de uma nova técnica para desengomar fibras da seda foi descrito no artigo "Some Studies in Degumming of Silk with Organic Acids" ( J . Society of Dy
a. Quando o modelo Y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 1 2 + β 4 x 2 2 + β 5 x 1 x 2 + ϵ é ajustado aos dados sobre lúpulo do Exercício 49, a estimativa de β 5 é β ˆ 5 = 0,557 c o m um desvio padrão e
O projeto eficaz de determinados tipos de incineradores de lixo municipal necessita de informaçôes sobre o conteúdo de energia do lixo. Os autores do artigo "Modeling the Energy Content of Municipal S