Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 48
Um experimento realizado para investigar os efeitos de uma nova técnica para desengomar fibras da seda foi descrito no artigo "Some Studies in Degumming of Silk with Organic Acids" ( . Society of Dyers and Colourists, 1992, p. 79-86). Uma variável de resposta de interesse foi perda de peso (%). Os pesquisadores fizeram observações sobre a perda de peso para vários valores de três variáveis independentes: temperatura tempo de tratamento (min.) concentração de ácido tartárico . Nas análises de regressão, os três valores de cada variável foram codificados como e 1 , respectivamente, gerando os dados a seguir (o valor foi indicado, mas nosso valor 20,3 produziu um resultado de regressão idêntico ao reproduzido nesse artigo)
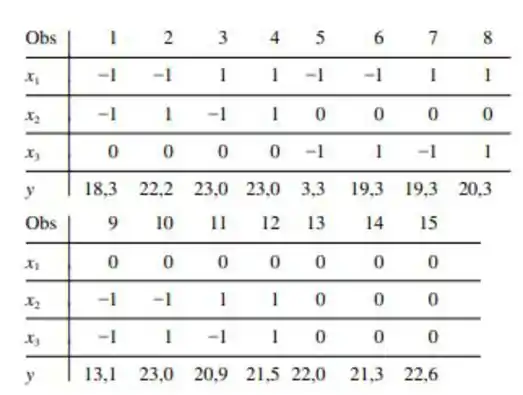
Um modelo de regressão múltipla com previsores - foi ajustado aos dados, gerando , ,
a. Esse modelo indica uma relação útil? Expresse e teste as hipóteses apropriadas usando um nível de significância de 0,01 .
b. desvio padrão estimado de quando (isto é, quando a temperatura , tempo e concentração ) é 1,248. Calcule um IC de para a perda de peso esperada em relação aos valores especificados da temperatura, do tempo e da concentração.
c. Calcule um IP de para um único valor de perda de peso a ser observado em relação aos valores 100 , 75 e 8 de temperatura, tempo e concentração, respectivamente.
d. Ajustando o modelo com apenas e como previsores, obtemos e . Existe uma relação útil entre a perda de peso e pelo menos um dos previsores de segunda ordem , ? Expresse e teste as hipóteses apropriadas.
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Esse modelo indica uma relação útil? Expresse e teste as hipóteses apropriadas usando um nível de significância de 0,01 .
a.
pelo menos umRR:
Falha ao rejeitar . O modelo não parece especificar um relacionamento útil.
Passo 2
desvio padrão estimado de quando (isto é, quando a temperatura , tempo e concentração ) é 1,248. Calcule um IC de para a perda de peso esperada em relação aos valores especificados da temperatura, do tempo e da concentração.
b. , então a C.I. é
Passo 3
Calcule um IP de para um único valor de perda de peso a ser observado em relação aos valores 100 , 75 e 8 de temperatura, tempo e concentração, respectivamente.
c. , e a C.I. é
Passo 4
Ajustando o modelo com apenas e como previsores, obtemos e . Existe uma relação útil entre a perda de peso e pelo menos um dos previsores de segunda ordem , ? Expresse e teste as hipóteses apropriadas
: pelo menos um dos acima RR:
Rejeite . Pelo menos um dos preditores de segunda ordem parece útil.
Resposta
a. Falha ao rejeitar . O modelo não parece especificar um relacionamento útil.
b.
c.
d. Rejeite . Pelo menos um dos preditores de segunda ordem parece útil.
Espero que tenham aprendido com essa questão, até a próxima !