Calcule uma tabela de ANOVA para os efeitos e teste a curvatura com . A curvatura é importante nessa região dos fatores?
Calcule os resíduos a partir do modelo linear e teste a adequação de seu modelo.
Em uma nova região do espaço de fatores, um planejamento composto central (PCC) foi usado para fazer uma otimização de segunda ordem. OS resultados são mostrados na tabela seguinte. Ajuste um moledo de segunda ordem a esses dados e tire conclusões.
Passo 1
Bom galera, considere um nível baixo e é um nível alto do primeiro fator , e um nível baixo e um nível alto do segundo fator . O ponto é o ponto central. Portanto, nós temos um experimento fatorial com valores no ponto central.
Vamos encontrar os efeitos estimados, temos como o fator de e o fator de . Para o experimento fatorial temos a tabela:

Passo 2
Belezinha, agora usando a tabela de sinais para calcular o efeito de . Adicionando os efitos com os sinais correspondentes na coluna do fator considerado.
Todos os outros efeitos são encontrados da mesma forma. A tabela dos efeitos para todos os fatores é interações é dada por:
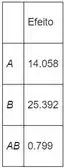
Agora realizando a analise das variâncias:
Passo 3
Show de bola, agora calculamos todas as somas dos quadrados e ficamos com:
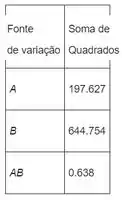
Calculamos as medias de observações e pontos de controle:
Calculamos
E a para curvatura:
Passo 4
Cada um por cada fator ou interação tem grau de liberdade, tem graus de liberdade, e tem grau de liberdade. Encontramos cada como a razão de e correspondentes. Encontramos também o total de e . O resultado está resumido na tabela:
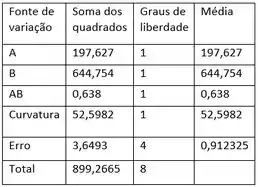
Passo 5
Encontraremos agora o valor de estatística para cada fator e interação como uma razão de correspondente para . O resultado está resumido na tabela abaixo. Usando o Minitab para encontrar os valores.
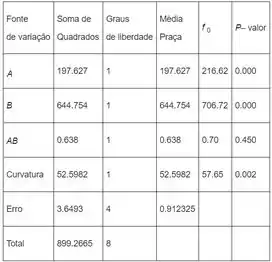
O valor do teste para curvatura é de , logo é inferior a , concluímos que há evidência de curvatura. O valor para o teste de significância de interação é superior a . Portanto, podemos concluir que a interação não é significativa. O valor para os teste dos efeitos são todos inferiores a , logo, concluímos que ambos tem efeito significante.
Passo 6
Agora vamos construir um modelo de regressão linear para os fatores e . Os repressores e são codificados por e para níveis baixos e altos de fatores e por para o ponto central. A constante é estimada pela grande média, e os coeficientes de regressão são estimados pela metade das estimativas de efeito correspondente. O modelo de regressão fica:
O valor ajustado e o residual para primeira observação são:
Passo 7
Os resíduos calculados ficam:
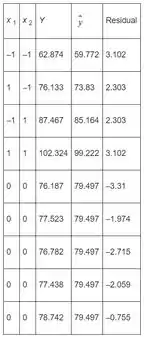
Então usamos o Minitab para plotar os gráficos de probabilidade normal e os lotes de resíduos pelo valor montado e cada regressor. Temos então:
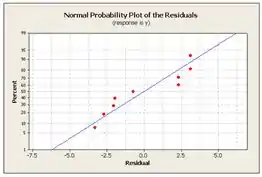
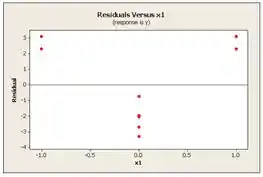
Os pontos não estão na linha. Portanto, podemos concluir que a suposição de erro normal é violada. Além disso, os lotes de residuos mostram que há violação da suposição de variancias iguais, logo concluimos que o modelo linear não é adequado.
Passo 8
Por fim, vamos considerar modelo para observações e em notação matricial. Para obter o modelo de regressão escrito em deve ser usada a formula:
O vetor de resíduos é dado por:
O estimador da variância é:
E usando o Minitab para encontrar a equação de regressão temos:
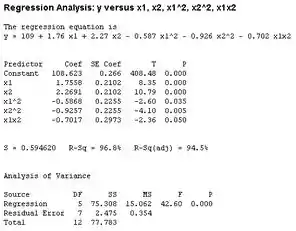
A partir disso vemos que todos os termos são significativos e o modelo de segunta ordem é:
Então usamos o Minitab para plotar os gráficos de probabilidade normal e os lotes de resíduos pelo valor montado e cada regressor. Temos então:
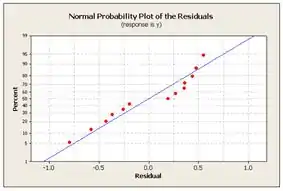
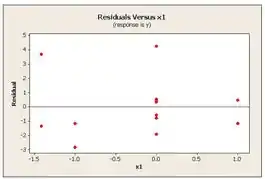
Os pontos no estão mais próximos da linha do que para o modelo linear mas ainda não estão perto o suficiente. As parcelas residuais ainda indicam violação da suposição de variancias iguais. O modelo não é adequado.
Resposta
Concluímos que ambos tem efeito significante.
Concluimos que o modelo linear não é adequado.
O modelo não é adequado.