Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 2.Exercícios - Ex. 115

O circuito a seguir opera se, e somente se, houver um caminho de dispositivos funcionais, da esquerda para a direita. A probabilidade de cada aparelho funcionar é mostrada. Suponha que a probabilidade de um dispositivo ser funcional não dependa de os outros dispositivos serem ou não funcionais. Qual será a probabilidade de o circuito operar?

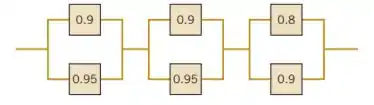
Passo 1

Vamos fazer com que o primeiro par de dispositivos seja U 1 ,   L 1 , o segundo par de dispositivos seja U 2 ,   L 2 e o terceiro par de dispositivos seja U 3 ,   L 3 ( U   significa superior e L significa inferior).

A condição necessária para o circuito operar é:

( U 1 ou L 1 funcionam) e ( U 2 ou L 2 funcionam) e ( U 3 ou L 3 funcionam).

Esta condição é dada no texto do exercício. Agora usamos a regra geral da adição para calcular:

P ( U 1 o u   L 1 f u n c i o n a m )   =   P ( U 1   f u n c i o n a ) + P ( L 1   f u n c i o n a ) - P ( U 1 f u n c i o n a   e   L 1 f u n c i o n )

Passo 2

Agora, a partir da independência mútua dos dispositivos, obtemos:

P ( U 1 e   L 1 f u n c i o n a m )   = P ( U 1 f u n c i o n a ) P ( L 1 f u n c i o n a ) = 0.095 × 0.9

Só inserir isso acima e calcular:

P ( U 1 o u   L 1   f u n c i o n a ) = 0.9 + 0.95 - 0.9 × 0.95 = 0.995

Exatamente da mesma maneira, obtemos:

P ( U 2 o u   L 2   f u n c i o n a ) = 0.995

P ( U 3 o u   L 3   f u n c i o n a ) = 0.98

Passo 3

Por fim, use a independência para combinar estes 3 resultados:

P ( c i r c u i t o   o p e r a ) = 0.995 × 0.995 × 0.98 = 0.97022

Resposta

0.97022

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em testes de placas de circuitos, a probabilidade de falha em um diodo é de 0,01. Suponha que uma placa de circuito contenha 200 diodos. a. Quantos diodos espera-se que apresentem falhas e qual é o de
Suponha que pequenas aeronaves pousem em um aeroporto, de acordo com um processo de Poisson, com a taxa 8 por hora, de forma que o número de pousos durante um período de tempo de t horas é uma va de P
Suponha que as árvores sejam distribuídas em uma floresta de acordo com um processo bidimensional de Poisson com parâmetro ∝ . O número esperado de árvores por acre é igual a 80. a. Qual é a probabili
O artigo “Reliability-Based Service-Life Assessment of Aging Concrete Structures” (J. Structural Engr., 1993, p. 1600-1621) sugere que um processo de Poisson pode ser usado para representar a ocorrênc
Seja X uma distribuição de Poisson com parâmetro . Demonstre que E(X) diretamente da definição de valor esperado. (Sugestão: O primeiro termo da soma é igual a 0, então x pode ser cancelado. Fatore e