Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 14.Exercícios Suplementares - Ex. 44

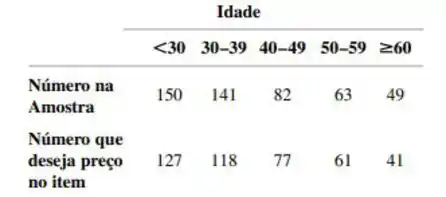
Muitos compradores expressaram desagrado porque as lojas deixaram de colocar preços nos itens individuais. artigo "The Impact of Item Price Removal on Grocery Shopping Behavior"(J. Marketing, 1980, p. 73-93) informa sobre um estudo no qual cada comprador em uma amostra foi classificado por idade e se ele ou ela sentiam a necessidade do preço no item. Baseado nos dados correspondentes, a necessidade do preço do item aparecer é independente da idade?

Passo 1

E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

Baseado nos dados correspondentes, a necessidade do preço do item aparecer é independente da idade?

A tabela a seguir contém contagens esperadas observadas e estimadas, esta última entre parênteses.

Isso dá.

No nível 0,05, a hipótese nula de independência é rejeitada, embora não seja rejeitada no nível 0,01 (0,01

Resposta

embora não seja rejeitada no nível 0,01 (0,01

Espero que tenham aprendido com essa questão, até a próxima !

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Uma amostra de 200 estudantes que realizaram testes biométricos apresentou a distribuição abaixo. Ajudar uma distribuição normal a esses dados e efetuar o teste de aderência, para α = 0,05 .

Os últimos algarismos de sessenta números telefônicos consecutivos, extraídos de uma página das listas telefônica, foram:Testar se o aparecimento dos números é equiprovável, para α = 0,05

Uma amostra de 5 0 parafusos produzidos por uma máquina forneceu a distribuição de frequência abaixo. Ajustar uma distribuição normal e efetuar o teste de aderência, com α = 0,02 .

Uma urna contém um grande número de bolas brancas, pretas, azuis, amarelas, verdes e vermelhas. Foram retiradas 100 bolas ao acaso e encontramos 36 brancos, 21 pretas, 7 azuis, 12 amarelas, 10 verdes

Três moedas desconhecidas foram lançadas 200 vezes, anotando-se o número de coroas surgidas em cada lançamento. Para α = 0,05 , testar a hipótese de que as moedas são honestas ajustando uma binomial.