Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 14.Exercícios Suplementares - Ex. 46
. O torneio de basquete da NCAA inicia com 64 times que são divididos em quatro torneios regionais, cada um envolvendo 16 times. Estes, em cada região, são então classificados (espalhados) de 1 a 16. Durante o período de 12 anos de 1991 até 2002, o time no topo da classificação venceu seu torneio regional 22 vezes, o time classificado em segundo lugar venceu 10 vezes, o time classificado no terceiro lugar venceu 5 vezes e os 11 torneios regionais remanescentes foram vencidos pelos times classificados abaixo de 3 . Represente por a probabilidade que o time classificado como em sua região seja vitorioso em seu jogo contra o time classificado como . Uma vez que os s estejam disponíveis, é possível calcular a probabilidade de que cada classificado particular vença seu torneio regional (um cálculo amostral é um tanto grande). O artigo "Probability Models for the NCAA Regional Basketball Tournaments" (The American Statistician, 1991, p. 35-38) propõe vários modelos diferentes para os S.
a. Um modelo postulou (a partir do qual etc.). Baseado nisto, (classificado em primeiro lugar vence (classificado segundo lugar vence) e (classificado em terceiro lugar vence) . Este modelo parece fornecer um bom ajuste aos dados?
b. Um modelo mais sofisticado tem , onde os zs são medidas de resistência relativa relacionadas com percentuais normais padronizados (percentis para times sucessivos altamente classificados estão mais próximos do que o caso dos times com a classificação mais baixa, e 0,2813625 garante que a variação de probabilidades seja a mesma como para o modelo na parte (a)). As probabilidades resultantes das classificações 1,2 ou 3 de vencer seus torneios regionais são 0,45883, 0,18813 e 0,11032 , respectivamente. Calcule o ajuste deste modelo.
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Um modelo postulou (a partir do qual etc.). Baseado nisto, (classificado em primeiro lugar vence (classificado segundo lugar vence) e (classificado em terceiro lugar vence) . Este modelo parece fornecer um bom ajuste aos dados?
a.
: probabilidades são as especificadas. : probabilidades não são as especificadas..Teste estatístico: . Região de rejeição: uma vez que , rejeitamos . O modelo postulado no exercício não é um bom ajuste.
Passo 2
b. Um modelo mais sofisticado tem , onde os zs são medidas de resistência relativa relacionadas com percentuais normais padronizados (percentis para times sucessivos altamente classificados estão mais próximos do que o caso dos times com a classificação mais baixa, e 0,2813625 garante que a variação de probabilidades seja a mesma como para o modelo na parte (a)). As probabilidades resultantes das classificações 1,2 ou 3 de vencer seus torneios regionais são 0,45883, 0,18813 e 0,11032 , respectivamente. Calcule o ajuste deste modelo.
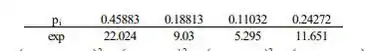
Com a mesma região de rejeição de a, não rejeitamos a hipótese nula. Este modelo oferece um bom ajuste.
Resposta
O modelo postulado no exercício não é um bom ajuste.
b. Com a mesma região de rejeição de a, não rejeitamos a hipótese nula. Este modelo oferece um bom ajuste.
Espero que tenham aprendido com essa questão, até a próxima !