Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 10.Exercícios - Ex. 19
Considere um experimento ANOVA de fator único no qual I = 3, J = 5, x = 10, x = 12, e x = 20. Encontre um valor de SQE para o qual , de modo que H0: 1 2 3 seja rejeitada, embora, quando se aplique o procedimento de Tukey, nenhum dos i possa ser considerado significativamente diferente entre si.
Passo 1
Sendo
A soma total dos quadrados (SST), tratamento soma de quadrados (SSTr), e erro soma dos quadrados (SSE) são dados por
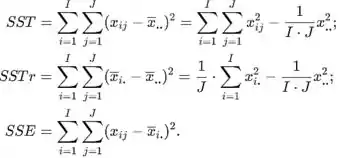
Os quadrados médios são
F é a razão dos dois quadrados médios
No exercício, os seguintes valores são dados
Os graus de liberdade da estatística F que é testada usando ANOVA de fator único são
Primeiro calcular
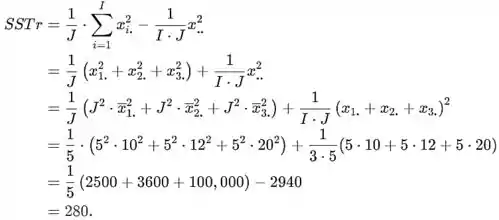
Passo 2
Agora, o MSTr é
O valor f é
A primeira condição é
Onde que pode ser obtido usando a tabela no apêndice; portanto
Ou
No entanto, tenha cuidado, esta não é a única condição! Lembre-se do seguinte:
Encontre o valor na Tabela A.10. no apêndice do livro para dado . Calcule e e liste as médias amostrais em ordem crescente. Calcule
e sublinhe os pares das médias da amostra que diferem em menos de w. O par de amostras que não são sublinhados pela mesma linha correspondente à população ou tratamento significa que são significativamente diferentes.
Passo 3
A partir disso, outra condição pode ser obtida para que, quando aplicado o procedimento de Turkey, nenhuma das médias seja estatisticamente diferente uma da outra. Da mesa
portanto, outra condição para SSESSE pode ser obtida de
É necessário que todas as diferenças médias sejam menores que w; assim, basta tomar o valor máximo das diferenças médias e torná-lo w maior que esse valor. A diferença máxima é
Portanto, a segunda condição é
Ou igualmente
Ou finalmente
A resposta pode ser qualquer número real SSE que satisfaça o seguinte