Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 53
Considere os quatro intervalos a seguir com base nos dados do Exemplo 12.4 (Seção 12.2): a. Um IC de 95% para uma porosidade média quando o peso unitário é 110. b. Um IP de 95% para uma porosidade em que o peso unitário é 110. c. Um IC de 95% para uma porosidade média quando o peso unitário é 115. d. Um IP de 95% para uma porosidade em que o peso unitário é 115. Sem calcular nenhum desses intervalos, o que se pode dizer sobre as amplitudes relativas entre um e outro?
Passo 1
A variância da variável aleatória é
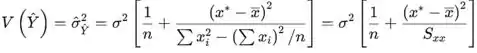
O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) por s você obtém a estimativa da variância e/ou desvio padrão da variável aleatória Um intervalo de confiança de para a média de Y quando
Passo 2
é um intervalo de previsão de para uma observação futura Y, quando
Como 110 está mais próximo da média do que 115, o intervalo de confiança (a)(a) será o menor (o intervalo de confiança é mais estreito que o intervalo de previsão). Da mesma forma, como o intervalo de previsão é mais amplo que o intervalo de confiança, o intervalo de previsão em (d) será o maior.
Usando o mesmo raciocínio, o intervalo em (a) é o intervalo menor (b); intervalo em (c) é menor que o intervalo em (d).
Entretanto, a relação entre os intervalos (b) e (c) não é óbvia; assim, não faça suposições sobre eles sem calcular os intervalos.
Resposta
CI em (a) é o menor; PI em d) é o maior