Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 14.Exercícios - Ex. 36
Considere a tabela correspondente mostrando as proporções da amostra que caem em várias combinações de categorias (por exemplo, 13\% daqueles na amostra que estavam na primeira categoria de ambos os fatores).
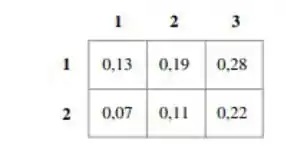
a. Suponha que a amostra considerada seja de pessoas. Utilize o teste qui-quadrado para independência com nível de significância 0,10 .
b. Repita a parte (a) assumindo que o tamanho da amostra foi de .
c. Qual é o menor tamanho de amostra para a qual estas proporções observadas resultarão na rejeição da hipótese de independência?
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
a. a. Suponha que a amostra considerada seja de pessoas. Utilize o teste qui-quadrado para independência com nível de significância 0,10 .
. Porque não é rejeitado.
Passo 2
b. Cada contagem de observação aqui é 10 vezes o que era em a, e o mesmo é verdadeiro para as contagens esperadas estimadas, então agora , e é rejeitado. Com o tamanho da amostra muito maior, o desvio do esperado sob , a hipótese de independência, é estatisticamente significativo - não pode ser explicado apenas pela variação aleatória.
Passo 3
c. As contagens observadas são .13n,.19n,.28n,.07n,.11n,.22n, enquanto a estimativa esperada , produzindo será rejeitado no nível .10 se . , i.e., se , então o mínimo
Resposta
a. não é rejeitado.
b. a hipótese de independência, é estatisticamente significativo - não pode ser explicado apenas pela variação aleatória.
c.
Espero que tenham aprendido com essa questão, até a próxima !