Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 14.Exercícios - Ex. 25

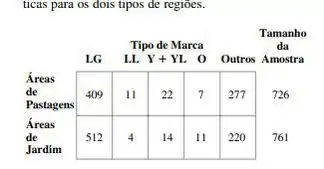
Os dados correspondentes referem-se a marcas de folhas encontradas em amostras selecionadas a partir de áreas de pastagens e jardins ("The Biology of the Leaf Mark Polymorphism in Trifolium repens L.", Heredity, 1976, p. 306-325). Utilize um teste χ 2 para decidir se as proposições verdadeiras de marcas diferentes são idênticas para os dois tipos de regiões.

Passo 1

E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

Utilize um teste χ 2 para decidir se as proposições verdadeiras de marcas diferentes são idênticas para os dois tipos de regiões.

Deixe P i j = a proporção de trevo branco na área do tipo i que tem uma marca do tipo j ( i = 1,2 ; j = 1,2 , 3,4 , 5 ). A hipótese H 0 : p 1 j = p 2 j for j = 1 , … , 5 será rejeitada no nível . 01 se χ 2 ≥ χ 01 , ( 2 - 1 ) ( 5 - 1 ) 2 = χ . 01,4 2 = 13.277

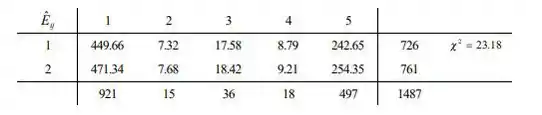
Uma vez que 23.18 ≥ 13.277 , H o é rejeitado.

Resposta

Uma vez que 23.18 ≥ 13.277 , H o é rejeitado.

Espero que tenham aprendido com essa questão, até a próxima !

Exercícios de Livros Relacionados

A tabela correspondente de entrada dupla foi construída utilizando-se dados do artigo "Television Viewing and Physical Fitness in Adults" (Research Quarterly for Exercise and Sport, 1990, p. 315-320).
Suponha que no Exercício 32 cada estudante tenha sido categorizado em relação a ponto de vista político, uso de maconha e preferência religiosa, com as categorias deste último fator sendo Protestante,
Suponha que em um estado com quatro regiões distintas, uma amostra aleatória de n k eleitores é obtida a partir da k -ésima região para k = 1,2 , 3 e 4. Cada eleitor é então classificado de acordo com
Cada indivíduo em uma amostra aleatória de estudantes da escola secundária e da faculdade foi classificado de maneira cruzada em relação a ponto de vista político e o uso de maconha, resultando nos da
Mostre que a estatística qui-quadrado para o teste de independência pode ser escrita na forma χ 2 = ∑ i = 1 l   ∑ j = 1 J   N i j 2 E ^ i j - n Por que esta fórmula é mais eficiente nos cálculos do qu