Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 24

Os dados a seguir foram reproduzidos de um gráfico apresentado no artigo “Reactions on Painted Steel Under the Influence of Sodium Chloride, and Combinations Thereof” (Ind. Engr. Chem. Prod. Res. Dev., 1985, p. 375–378). A variável independente é a taxa de deposição (mg/m2 /d) de SO2 e a variável dependente é a perda de peso do aço (g/m2 ).

a. Elabore um gráfico de dispersão. O modelo de regressão linear simples parece razoável nessa circunstância? b. Calcule a equação da reta de regressão estimada. c. Que porcentagem da variação observada na perda de peso do aço pode ser atribuída à relação do modelo com a variação na taxa de deposição? d. Pelo fato de o maior valor x na amostra ser sensivelmente maior do que os outros, essa observação pode ter influído muito na determinação da equação da reta estimada. Elimine essa observação e recalcule a equação. A nova equação parece diferir substancialmente da original (os valores previstos podem ser considerados)?

Passo 1

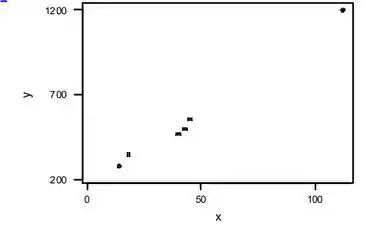
    2. De acordo com o gráfico de dispersão dos dados, um modelo de regressão linear simples parece ser plausível

  2. Nesta tarefa temos duas amostras com tamanho amostral n=6. Agora os valores necessários para esta amostra são fornecidos abaixo:

    3. β ^ 0 = y - - β ^ 1 x -

    = 560 - 9.311 ∙ 45.333

    = 137.876

    y ^ = 137.876 + 9.311 x

    Passo 2

  3. Agora precisamos encontrar a proporção da variação observada na remoção que pode ser explicada com este modelo. Esta proporção descreve o coeficiente de determinação r 2 , então precisamos encontrar esse valor. Temos a seguir

    4. Como podemos ver cerca de 99\%% desses dados, podemos descrever com este modelo de previsão

    Passo 3

  4. Agora vamos retirar o par (112, 1200) e então precisamos construir o modelo linear para predição deste conjunto de dados. A tabela é dada a seguir:

β ^ 0 = y - - β ^ 1 x -

= 432 - 7.55 ∙ 32

= 190.35

y ^ = 190.35 + 7.55 x

Agora precisamos encontrar a proporção da variação observada na remoção que pode ser explicada com este modelo. Esta proporção descreve o coeficiente de determinação r 2 , então precisamos encontrar esse valor. Temos a seguir

Como podemos ver cerca de 95% desses dados podemos descrever com este modelo de previsão.

Resposta

Ver o desenvolvimento.

Exercícios de Livros Relacionados

Foi feito o levantamento, com n = 12 pessoas, a respeito da idade Y , em função da respectiva altura X 1 (em cm) e do respectivo peso X 2 (em kg).Efetuando os cálculos dos somatórios necessários à mon
Uma empresa produz sapatos do tipo popular, numa quantidade anual vendida Y (em mil unidades). Pretende-se verificar a relação entre essa quantidade vendida e o preço relativo da única concorrente exi
Uma empresa produz sapatos do tipo popular, numa quantidade anual vendida Y (em mil unidades). Pretende-se verificar a relação entre essa quantidade vendida e o preço relativo da única concorrente exi
Uma empresa produz sapatos do tipo popular, numa quantidade anual vendida Y (em mil unidades). Pretende-se verificar a relação entre essa quantidade vendida e o preço relativo da única concorrente exi
Segundo dados da CESP, foi feito um levantamento, em n = 19 cidades do estado de São Paulo, a respeito da extensão da rede de transmissão urbana Y (em km de rede), em função da população economicament