As estatísticas resumidas a seguir foram obtidas de um estudo que usou a análise de regressão para investigar a relação entre a deflexão de pavimento e a temperatura da superfície do pavimento de vários lugares em uma rodovia estadual. Aqui, x temperatura (°F) e y fator de ajuste de deflexão (y 0
Passo 1
- Linha de regressão geral:
- A inclinação representa o aumento médio (ou diminuição quando negativo) da variável y por unidade de x.
- Seja o novo x
- Só é adequado estimar o valor y para um determinado valor de x quando o valor x estiver no intervalo dos valores x dados usados para calcular a equação de regressão (pois o padrão entre x e y pode mudar fora do intervalo de dados x-valores).
Vamos estimar a inclinação e a interceptação y da linha de regressão:

Substituindo por e por na linha de regressão geral:
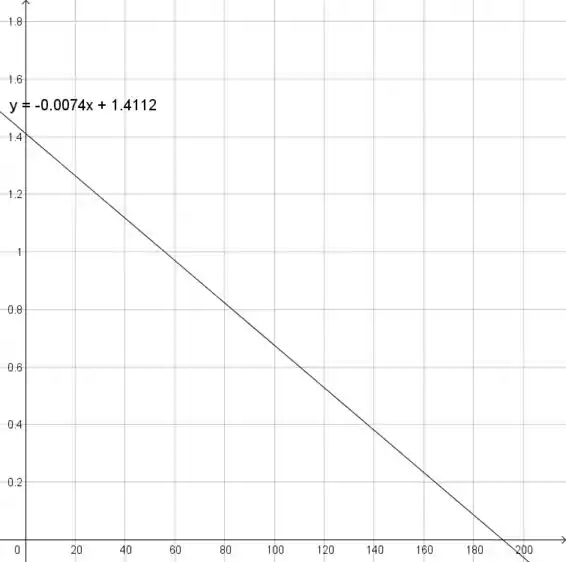
Passo 2
Isso implica que o fator de ajuste de deflexão deve diminuir em 0.00736 quando a temperatura é aumentada em
Desde
Substituindo x pela equação acima na equação da parte (a):
A inclinação representa o aumento médio (ou diminuição quando negativo) da variável y por unidade de x.
Isso implica que o fator de ajuste de deflexão deve diminuir em 0.013248 quando a temperatura é aumentada em
Passo 3
Assim, só será apropriado prever o fator de deflexão para uma temperatura de , quando estiver na faixa de temperaturas dadas usadas para calcular a equação de regressão.
Resposta
- , diminuição de 0.013248
- Será apropriado prever o fator de deflexão para uma temperatura de 200° F, quando 200° F estiver na faixa de temperaturas dadas usadas para calcular a equação de regressão