Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 1.Exercícios - Ex. 19
Os dados a seguir representam a duração da vida útil, em anos, medidos do décimo mais próximo, de 30 bombas de combustível:
(a) Construa um diagrama de ramo-e-folhas para a vida, em anos, das bombas de combustível, usando o dígito à esquerda da vírgula decimal como ramo para cada observação.
(b) Estabeleça a distribuição de frequências relativas.
(c) Calcule a média, a amplitude e o desvio-padrão amostrais.
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Vamos fazer o item a) onde nos é pedido o diagrama de ramo-e-folhas.
Desse modo, temos:
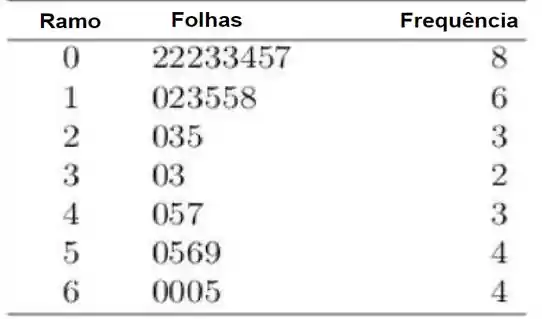
Passo 2
Agora vamos ao item b)
Nesse item iremos fazer uma tabela com intervalo de classe; ponto médio de classe; frequência e frequência relativa.
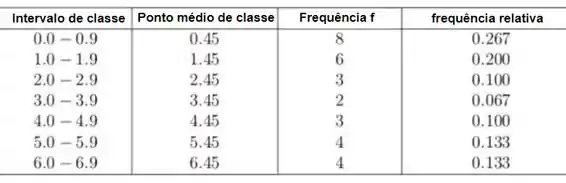
Passo 3
E por fim, vamos calcular a média a amplitude e o desvio padrão amostrais.
Calculando a média:
Calculando o desvio padrão:
Usando a relação entre variância e desvio padrão:
Por fim, vamos calcular a amplitude:
Resposta
a) vide gráfico.
b) vide gráfico.
c)