Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 3.Problemas - Ex. 19
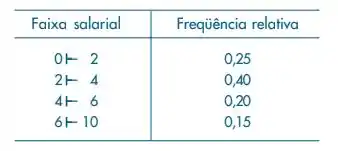
O Departamento Pessoal de uma certa firma fez um levantamento dos salários dos funcionários do setor administrativo, obtendo os resultados (em salários mínimos) da tabela abaixo.
Esboce o histograma correspondente.
Calcule a média, a variância e o desvio padrão.
Calcule o 1o quartil e a mediana.
Se for concedido um aumento de para todos os funcionários, haverá alteração na média? E na variância? Justifique sua resposta.
Se for concedido um abono de dois salários mínimos para todos os funcionários, haverá alteração na média? E na variância? E na mediana? Justifique sua resposta.
Passo 1
Bom galera, vamos começar esboçando o histograma:
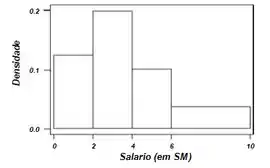
Passo 2
Show de bola, agora, vamos calcular a média, variância e o desvio padrão:
Mas não se esqueça que a frequência dada foi a frequência relativa, e precisamos transforma-la em frequência absoluta:
Agora sim, vamos encontrar a média
Para calcular a variância, usamos
Beleza?! Substituindo os valores,
Assim,
O desvio padrão é a raiz quadrada da variância:
Passo 3
Belezinha, encontramos o quartil e a mediana:
A mediana é:
Passo 4
Então, se todos os salários aumentarem em (dobrarem), a média dos salários dobrará, e assim, a variância será vezes maior. Pois, a diferença entre a média e todos os valores dobraram, e como a variância é ao quadrado, a variância é quadruplicado.
Já, caso todos os funcionários recebessem um abono de salários mínimos, a média e a mediana aumentariam em salários mínimos, mas o desvio padrão e a variância não se alteram, pois a média e todas observações sobem o mesmo valor, portanto a diferença entre eles permanece igual, logo a variância e o desvio padrão também.
Resposta
; ;
;