Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 3.Problemas - Ex. 18
O número de divórcios na cidade, de acordo com a duração do casamento, está representado na tabela abaixo.
Qual a duração média dos casamentos? E a mediana?
Encontre a variância e o desvio padrão da duração dos casamentos.
Construa o histograma da distribuição.
Encontre o e o decis.
Qual o intervalo interquantil?
Passo 1
Bom galera, vamos começar calculando a media de duração dos casamento, bem assim:
Enquanto que a mediana é a média dos elementos e , que é igual a:
Passo 2
Show de bola, agora, vamos para a variância e para o desvio padrão, primeiro a variância:
Agora, o desvio padrão é muito fácil, é só pegar a raiz quadrada da variância:
Passo 3
Belezinha, tá quase acabando, vamos plotar um histograma de distribuição, que fica assim:
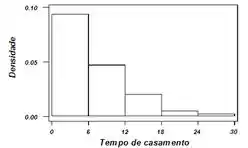
Passo 4
Por fim, a gente calcula o e o decil, também o intervalo interquantil, calma, é bem facinho, vamos começar com os dois decis:
E para o intervalo interquantil, nós precisamos calcular o eo quantil:
Então, o intervalo interquantil fica:
Resposta
;
;
;