Exercícios de 1º, 2º e 3º Quartil e Distância Interquartil - Lista de Exercícios Resolvida

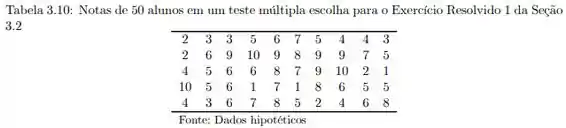
Considere novamente as notas dos 50 alunos, reproduzidas na Tabela 3.10. Calcule o intervalo interquartil das notas.

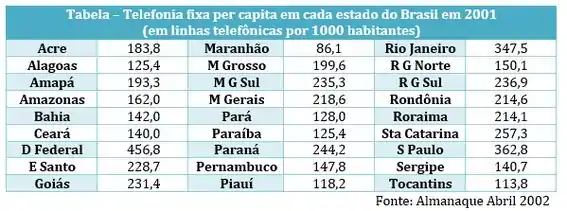
A tabela de dados brutos a seguir reporta, o número de linhas telefônicas por 1000 habitantes em cada estado do Brasil, em 2001.

b) Determine os seus quartis

Dado um conjunto de pares , variando de 1 até .

1. Que relação existe entre as médias das variáveis e , onde é uma constante (isto é, )? E entre as variâncias de e ? E entre as distâncias interquartis (DIQ) de e ? Qual o coeficiente de correlação de e ?
2. Responda as mesmas quatro perguntas do item (a) se , onde é uma constante positiva.

Um determinado fabricante produz implantes mamários utilizando gel de silicone. Os dados a seguir se referem a tensão de ruptura desses implantes e foram obtidos através de testes físicos realizados com uma amostra de tamanho n=20:

Com base nesses dados obtenha os quartis Q1,Q2 e Q3.

Foi apresentada a seguinte solução:

Posição (Q2)=

Posição (Q1) =

Posição (Q3) =

a) Algo está errado nessa solução. O que é?

b) Qual a solução correta?

Os dados abaixo correspondem a notas de uma turma de Probest com 30 alunos:

Onde:

(b)

(i) Calcule a média e os quartis;

(ii) Calcule a variância e o desvio padrão;

(iii) Existe alguma nota fora do intervalo ?

No processo de modelagem de um problema, sabe-se que determinada variável tem uma distribuição de probabilidade simétrica. Entretanto há controvérsias sobre se ela deve ser uma Uniforme ou uma Normal. Considere as variáveis aleatórias e , tais que e . Para comparar as distribuições de e de , calcule:

a)

b)

c) , (, significa distância interquartil).

Para o seguinte conjunto de dados ordenados: calcule as medidas de localização ou tendência central:

1. Mediana
2. Moda
3. Segundo decil
4. Primeiro quartil
5. Octogésimo terceiro percentil

Observação: Mostre os cálculos das posições das medidas de localização.

O comprimento das peças produzidas por uma máquina pode ser tratado como uma variável aleatória Normal com valor esperado µ (mm) e variância (mm2 ). Uma peça pode ser considerada defeituosa se o seu comprimento diferir do valor esperado mais do que σ. Sabe-se que 50% das peças produzidas têm comprimento inferior a 2,5 mm e 47,5% das peças produzidas têm comprimento entre 2,5 mm e 3,42 mm.

(a) Calcule µ e σ.

(b) Determine a probabilidade de que uma peça não seja defeituosa.

(c) Calcule DIQ, distância interquartil da v.a. comprimento das peças.

O tempo (em horas) necessário para reparar uma máquina é uma variável aleatória Exponencialmente distribuída com parâmetro .

(c) Calcule a Mediana () e Distância Interquartil (DIQ) de .

O tempo (em horas) necessário para reparar uma máquina é uma variável aleatória Exponencialmente distribu��da com parâmetro .

(d) Suponha agora que a distribuição do tempo () de reparo não seja mais Exponencial, mas que possa ser modelada por uma Normal com os mesmos parâmetros Média e Variância da Exponencial . Nesta nova condição calcule , Mediana() e DIQ().

Seja um conjunto de dados ordenados {7, 10, 30, 35, 50,52} , pede-se:

1. Mediana
2. Moda
3. Segundo decil
4. Primeiro quartil
5. Trigésimo quinto percentil

Observação: Deve-se identificar necessariamente a posição da estatística pedida.