Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 24
Deseja-se estimar qual a porcentagem média da receita familiar gasta com alimentação
pelos moradores de uma grande vila industrial. Para isso, selecionou-se uma amostra de
16 famílias, que apresentou os seguintes resultados:
41 44 35 42 34 22 42 42
38 62 29 63 38 45 48 40
(a) Dê um IC de 95% para a porcentagem média de todas as famílias de moradares da vila.
(b) Que suposição você fez para responder a pergunta anterior?
Passo 1
Primeiramente vamos definir X = porcentagem da receita familiar gasta com alimentação; e encontrar a média e a variância das amostras:
E
Com N=16 familias.
Devemos encontrar o Ic para a média de uma distribuição normal com variância desconhecida:
(distribuição t-student com n-1 graus de liberdade).
Passo 2
(a)
Onde
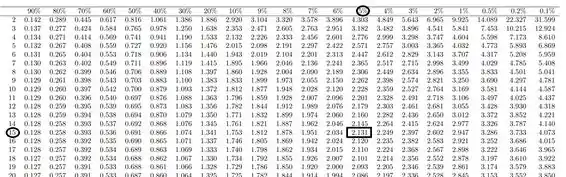
Lembrando que a tabela de t-student sempre mostra as porcentagens com p, como temos IC bilateral então , logo
Temos então:
Concluimos que a porcentagem média da receita famíliar gasta com alimentação está entre 36,05% e 47,07%.
Passo 3
(b)Supomos que a variável X segue uma distribuição normal com variância desconhecida, podendo ser aproximada por uma distribuição t-student com n-1 graus de liberdade.
Resposta
Ei, a resposta está no passo a passo :)