Determine o valor de c que faz a função ser uma função de probabilidades conjuntas em nove pontos com x = 1,2,3 e y = 1, 2,3.
Determine o seguinte:
- A distribuição de probabilidades marginais da variável aleatória X.
- A distribuição de probabilidades condicionais de Y, dado que X = 1.
- A distribuição de probabilidades condicionais de X, dado que Y = 2.
- X e Y são independentes?
Passo 1
Recebemos uma função de massa de probabilidade conjunta para . É sempre um bom começo escrever em uma tabela:

Primeiro, precisamos determinar o valor da constante c. A massa de probabilidade conjunta
função das variáveis aleatórias discretas X e Y satisfaz:
onde e são conjuntos de intervalos de variáveis aleatórias discretas, respectivamente, X e Y.
Usando isso, encontramos c da seguinte forma:
A tabela agora se torna:
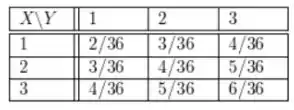
Passo 2
Letra a:
Para encontrar o P (X = 1, Y
Passo 3
Letra b:
Da mesma forma que acima, Y
Passo 4
Letra c:
Temos:
* a união é quase certa, embora possamos sempre cruzar com ela.
Passo 5
Letra d:
Isso só é possível quando e , então:
Passo 6
Letra e:
Antes de começarmos a encontrar os valores e lembre-se das definições:
A expectativa matemática da variável aleatória discreta X é a soma do produto final de cada possibilidade com sua probabilidade :
é a variância da variável aleatória X definida como:
Analogamente como em C, encontramos funções de massa marginal para X e Y:
A partir das definições acima, temos:
Para calcular observe que é uma variável aleatória discreta e que pode ser escrito como nós sabemos que:
Calculando isso, temos:
E as variações. da definição são:
Vamos ter cuidado ao arredondar os números, você pode precisar ser mais preciso!
Passo 7
Letra f:
Já calculamos a distribuição marginal de X, e é:

Passo 8
Letra g:
Quando temos função de massa conjunta e distribuição marginal de X, podemos encontrar a condição de distribuição como:
Por exemplo:
Para todo encontramos os valores e obtemos:
![]()
Passo 9
Letra h:
De modo semelhante temos:
Encontramos todas as probabilidades (veja acima!). A probabilidade de distribuição condicional de é:
![]()
Passo 10
Letra i:
Nós já demos a definição de expectativa da questão G:
Passo 11
Letra j:
Aqui, precisamos verificar se as seguintes funções são iguais para todo :
Vamos pegar e , então temos:
que não é igual, e logo, não são independentes.
Resposta
- ¼
- ¼
- 12/36
- 2/36
- Ver resolução
- Ver resolução
- Ver resolução
- 20/9
- Eles não são independentes.