Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 37

Uma empresa de transporte de mercadorias por caminhão avaliou um modelo de regressão múltipla para relacionar a variável dependente y tempo de percurso diário total de um de seus motoristas (horas) com os previsores x1 distância percorrida (milhas) e x2 número de entregas feitas. Suponha que a equação do modelo seja

Passo 1

  1. Leia com atenção para determinar o que deve ser x 1 e o que deve ser x 2 - trocando esses dois, você não obteria o valor médio correto. Da função de regressão, e para

    2. x 1 = 50 ; x 2 = 3

    um obteria o valor médio de y

    O valor esperado é de 4.9 horas.

    Passo 2

  2. Da descrição dada do que x i representa, pode-se concluir que mantendo x 2   constante, número de entregas, a mudança média no tempo de viagem y aumentará em 0.060 horas (que é β 1 = 0.060 )   para cada aumento de 1 milha na distância.

    3. Pode-se concluir que mantendo x 1 constante, distância percorrida, a mudança média no tempo de viagem y aumentará em 0.900 horas (que é β 2 = 0.900 ) para cada 1 aumento de entrega extra.

  3. No exercício o desvio padrão é dado

σ = 0.5

que poderia ser usado para padronizar a variável aleatória Y para calcular a probabilidade necessária. O valor esperado foi calculado em (a); assim, vale o seguinte

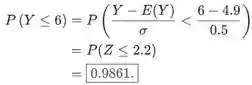
Resposta

Ver o desenvolvimento

Exercícios de Livros Relacionados

Em um experimento para avaliar os efeitos do tempo de tratamento (fator A ) e o tipo de mistura (fator B ) na resistência à compressão de cubos de cimento endurecido, três diferentes tempos de tratame
O artigo "Towards Improving the Properties of Plaster Moulds and Castings" (J. Engr. Manuf., 1991, p. 265269) descreve várias ANOVAs realizadas para investigar como a quantidade acrescida de fibra de
Em um estudo sobre os processos usados para remover impurezas de produtos de celulose ("Optimization of RopeRange Bleaching of Cellulosic Fabrics", Textile Research J., 1976, p. 493-496), foram obtido
O Artigo "An Analysis of Variance Applied to Screw Machines" (Industrial Quality Control, 1956, p. 8-9) descreve um experimento realizado para investigar como o comprimento das barras de aço era influ
No Exercício 39, suponha que, para obter os dados, tenha-se usado uma temperatura baixa de água. Todo o experimento é em seguida repetido com uma temperatura mais alta para obter os dados a seguir. Us