Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 11.Exercícios - Ex. 16

Em um experimento para avaliar os efeitos do tempo de tratamento (fator A ) e o tipo de mistura (fator B ) na resistência à compressão de cubos de cimento endurecido, três diferentes tempos de tratamento foram usados em conjunto com quatro diferentes misturas, obtendo-se três observações para cada uma das 12 combinações de tempo de tratamento/mistura. As somas de quadrados resultantes foram calculadas para ser S Q A = 30.763,0 , S Q B = 34.185,6 , S Q E = 97.436,8 e S Q T = 205.966,6

a. Elabore uma tabela ANOVA.

b. Teste no nível 0,05 a hipótese nula H 0 Λ B : todos os γ i j   s = 0 (sem interação de fatores) em relação à H a A B : pelo menos um γ i j ≠ 0

c. Teste no nível 0,05 a hipótese nula H 01 : α 1 = α 2 = α 3 = 0 (não existem efeitos principais do fator A ) em relação a H a A : pelo menos um α i ≠ 0 .

d. Teste H 08 : β 1 = β 2 = β 3 = β 4 = 0 versus H a B : pelo menos um β j ≠ 0 usando um nível de teste 0,05 .

e. Os valores dos x ‾ i . . foram x ‾ 1 . . = 4010,88 , x ‾ 2 . . = 4029,10 , e x ‾ 3 . = 3960,02 . Use o procedimento de Tukey para investigar diferenças significativas entre os três tempos de tratamento.

Passo 1

  1. E aí pessoal partiu para mais uma questão de probabilidade? Abaixo começaremos trazendo algumas informações do enunciado:

Elabore uma tabela ANOVA.

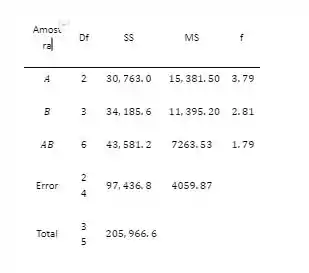
Passo 2

Teste no nível 0,05 a hipótese nula H 0 Λ B : todos os γ i j   s = 0 (sem interação de fatores) em relação à H a A B : pelo menos um γ i j ≠ 0

b. f A B = 1.79 a qual não é ≥ F . 05,6 , 24 = 2.51 , então H o A B não pode ser rejeitada, e concluímos que nenhuma interação está presente.

Passo 3

Teste no nível 0,05 a hipótese nula H 01 : α 1 = α 2 = α 3 = 0 (não existem efeitos principais do fator A ) em relação a H a A : pelo menos um α i ≠ 0 .

c. f A = 3.79 a qual é ≥ F . 05,2 , 24 = 3.40 , então H O A é rejeitado no nível .05.

Passo 4

Teste H 08 : β 1 = β 2 = β 3 = β 4 = 0 versus H a B : pelo menos um β j ≠ 0 usando um nível de teste 0,05

d. f B = 2.81 a qual não é ≥ F . 05,3 , 24 = 3.01 , então H o B não é rejeitado.

Passo 5

Os valores dos x ‾ i . . foram x ‾ 1 . . = 4010,88 , x ‾ 2 . . = 4029,10 , e x ‾ 3 . = 3960,02 . Use o procedimento de Tukey para investigar diferenças significativas entre os três tempos de tratamento.

e .   Q . 05,3 , 24 = 3.53 , w = 3.53 4059.87 12 = 64.93 .

2   4029.10  

Apenas os tempos 2 e 3 produzem forças significativamente diferentes.

Resposta

a. quadro acima

b. H o A B não pode ser rejeitada, e concluímos que nenhuma interação está presente.

c. H O A é rejeitado no nível .05.

d. 64.93 .

e. Apenas os tempos 2 e 3 produzem forças significativamente diferentes.

Espero que tenham aprendido com essa questão, até a próxima !

Exercícios de Livros Relacionados

Considere os dados do exercicio 11-7 sobre y=concentração do licor verde de Na2S e x=produção da maquina de papel. Suponha que o 14 pontos seja adicionado aos dados originais.(a)Prepare um diagrama da
a. Mostre que ∑ a   - 1 e i = 0 quando os e i s sao os resíduos de uma regressāo linear simples.b. Os resíduos de uma regressão linear simples são independentes entre si, positivamente correlacionados
À medida que a temperatura do ar cai, as águas dos rios ficam supercongeladas, formando cristais de gelo. Esse gelo pode influenciar significativamente a hidráulica de um rio. O artigo "Laboratory Stu
Suponha que as variáveis x = distância de comutaçāo e y = tempo de comutação estejam relacionadas de acordo com o modelo de regressāo linear simples, com σ = 10 .a. Se n = 5 observaçōes forem feitas n
Um experimento ANOVA de quatro fatores foi realizado para investigar os efeitos do tecido ( A ) , do tipo de exposiçāo ( B ) , do nivel de exposiçāo ( C ) e da direção das fibras ( D ) na intensidade