Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 30

O artigo “A Simulation–Based Evaluation of Three Cropping Systems on Cracking–Clay Soils in a Summer Rainfall Environment” (Agricultural Meteorology, 1976, p. 211–229) propõe um modelo quadrático para a relação entre o índice de abastecimento de água (x) e a produção de trigo de uma fazenda (y). A seguir são apresentados dados representativos e o resultado do MINITAB:

Passo 1

  1. O coeficiente de determinação, r 2 , pode ser encontrado na saída e é

    2. r 2 = 0.853

    ou igualmente, 85,3% da variação observada na densidade pode ser atribuída à relação do modelo.

  2. Nós estamos testando H 0   : β 2 = β 20 contra umas das outras alternativas, o valor estatístico é

    3. Dependendo da hipótese alternativa, o valor P pode ser determinado como área correspondente sob t n - k + 1

    O teste de uso é

    H 0   : β 2 = 0   v s   H a   : β 2 ≠ 0

    t = - 0.0010050 - 0 0.0001213 = - 8.29

    Com o valor P

    P = 2 P T > t = 0.015

    onde T tem distribuição de Student com n - ( k + 1 ) = 2 graus de liberdade. Desde

    P = 0.014 < 0.05 = α

    rejeitar hipótese nula em dado nível de significância α. O preditor quadrático fornece informações úteis.

    Passo 2

  3. Um intervalo de confiança de 100 ( 1 - α ) % para a média de Y quando x = x *

    4. y ^ ≠ t α 2 , n - k + 1 ∙ s Y ^

    onde

    e onde s Y ^ é o desvio padrão estimado de   μ ^ Y ∙ x * .

    Do exercício, quando x * =   100 , o valor ajustado é

    y ^ = 134.07

    e o desvio padrão estimado do valor ajustado (dado no exercício) é

    s Y ^ = 2.38

    A partir da tabela no apêndice pode-se encontrar o valor t

    Um intervalo de confiança de 100 ( 1 - α ) % para a média de Y quando x * = 100

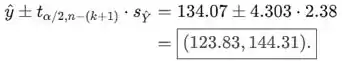
    Passo 3

  4. Intervalo de previsão

Onde

e onde s Y ^ é o desvio padrão estimado de   μ ^ Y ∙ x * é um intervalo de previsão de 100 1 - α % para uma observação futura Y, quando x   =   x * .

Como acima, quando x * = 100 , o valor ajustado é

y ^ = 134.07

e o desvio padrão estimado do valor ajustado é

s Y ^ = 2.38

A partir da tabela no apêndice pode-se encontrar o valor t

A estimativa do desvio padrão σ é

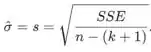
O desvio padrão estimado, s, é dado na saída

s 2 = 23.72 2 = 11.86 ;

portanto, um intervalo de previsão para observação futura quando x * = 100 é

Resposta

  1. r 2 = 0.853
  2. Rejeitar a hipótese nula
  3. 123.83,144.31
  4. ( 116.06,152.08 )

Exercícios de Livros Relacionados

A produção de uma máquina de extrusão contínua de revestimento de tubos de aço com plástico foi investigada como função do perfil de temperatura do termostato ( A , em três níveis), do tipo de plástic
a. Mostre que E X ‾ i . . - X ‾ . . = α i , de modo que X ‾ i . . - X ‾ … . . é um estimador não-tendencioso de α i (no modelo de efeitos fixos).b. Sendo γ ˆ i j = X ‾ i j - X ‾ j . . - X ‾ j . + X ‾
Os dados a seguir foram obtidos em um experimento realizado para investigar se a resistência à compressão de cilindros de concreto depende do tipo de material de revestimento usado ou da variabilidade
Mostre como um IC t 100 ( 1 - α ) % para α i - α i pode ser obtido. Em seguida, calcule um intervalo de 95 % para α 2 - α 3 usando os dados do Exercício 19. [Sugestāo: c o m ⁡ θ = α 2 - α 3 , o result
As curvas de potência das Figuras 10.5 e 10.6 podem ser usadas para obter β = P (erro do tipo II) no teste F na ANOVA de dois fatores. Para valores fixos de α 1 , α 2 … , α p , a quantidade ϕ 2 = ( J