Um escritório de investimento acredita que o rendimento das diversas ações movimenta-

das por ele foi de 24%. Mais ainda, a nova estratégia definida deve garantir uma maior

uniformidade nos rendimentos das diversas ações. No passado, o desvio padrão do

rendimento era da ordem de 5%. Para verificar as duas hipóteses, tomaram-se 8 empre-

sas ao acaso, obtendo-se os seguintes rendimentos (dados em %): 23,6; 22,8; 25,7; 24,8;

26,4; 24,3; 23,9 e 25. Quais seriam as conclusões?

Primeiramente, vamos realizar o teste para a variância, usando a seguinte aproximação:

(qui-quadrado, com graus de liberdade).

Teste de hipótese:

Vamos construir a Região crítica: RC={

Onde: 2,167

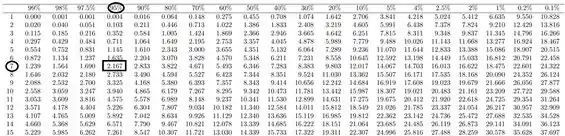
Portanto nossa Região crítica assume a seguinte forma:

Teste sob

Como , rejeitamos , e então temos evidencias de que a variância mudou com a nova estratégia.

Agora temos de testar a média, considerando que a variância é desconhecida, temos a seguinte aproximação:

Teste de hipótese:

Novamente precisamos construir nossa região critica:

Onde:

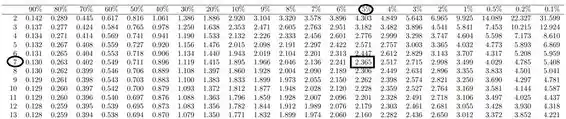
Lembrando que na distribuição de t-student, quando temos uma RC bilateral

Logo, nossa região crítica assume a seguinte forma:

Teste sob

Temos então não pertence à Região crítica, não devemos rejeitar , portanto a suspeita do escritório estava correta.