Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 36
Um fabricante de um certo tipo de aço especial afirma que seu produto tem um severo
serviço de controle de qualidade, traduzido pelo desvio padrão da resistência à tensão,
que não é maior do que 5 kg por cm2. Um comprador, querendo verificar a veracidade da
afirmação, tomou uma amostra de 11 cabos e submeteu-a a um teste de tensão. Os
resultados foram os seguintes: = 263 e = 48. Estes resultados trazem alguma evidência
contra a afirmação do fabricante? Use α = 0,05.
Passo 1
Do enunciado:
X = resistência à tensão
N = 11 cabos
= 263 kg/ e = 48
Considerando com
Vamos realizar o teste de hipótese para variância:
.
Passo 2
Teste de hipótese:
Vamos primeiramente construir nossa região crítica:RC={
Onde
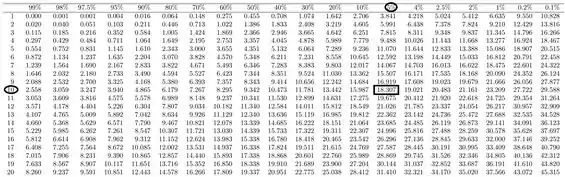
Lembrando que na tabela de distribuição qui-quadrado quando o limite é unilateral superior(definido pela hipótese alternativa que apresenta o sinal “>”).
Portanto a Região crítica fica definida assim: RC={}
Passo 3
Teste sob
Obs: o teste sempre é feito sobre a hipótese nula, pois ela apresenta igualdade(
Resposta
Como, podemos rejeitar e concluir que há evidencias de que o desvio-padrão é maior do que 5, contrariando a afirmação do fabricante.