Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 17
Os novos operários de uma empresa são treinados a operarem uma máquina, cujo
tempo X (em horas) de aprendizado é anotado. Observou-se que X segue de perto a
distribuição N(25, 100). Uma nova técnica de ensino, que deve melhorar o tempo de
aprendizado, foi testada em 16 novos empregados, o quais apresentaram 20,5 horas
como tempo médio de aprendizado. Usando o valor-p, você diria que a nova técnica é
melhor que a anterior?
Passo 1
Do exercício, temos:
X = tempo de aprendizado(horas).
Após a aplicação da nova técnica =>
Devemos realizar o teste da média para uma população com variância conhecida().
Temos então:
Passo 2
Teste de Hipótese:
Obs: a hipótese alternativa() visa responder a seguinte pergunta: “A nova técnica é melhor?”
Considerando vamos realizar o teste sob ().
Lembrando que o teste sempre é realizado sob , uma vez que a hipótese nula sempre vai levar o sinal de igual ().
Passo 3
Procurando na tabela de Distribuição normal encontramos o valor de -1,64 que corresponde a probabilidade .
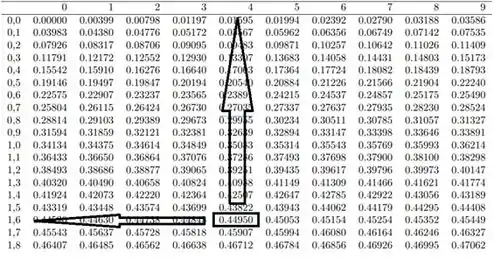
Lembrando que o negativo no -1,64 remete a hipótese alternativa definida por nós, definida com o sinal de “
Para encontrarmos o p-valor devemos buscar na tabela a probabilidade de 1,80.
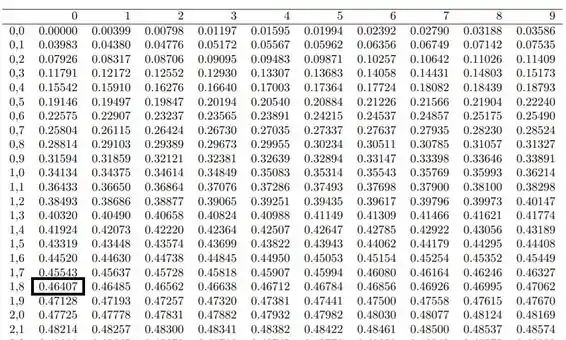
Resposta
Como p-valor