Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 4.Problemas - Ex. 18
No estudo de uma certa comunidade, verificou-se que:
(I) A proporção de indivíduos solteiros é de 0,4.
(II) A proporção de indivíduos que recebem até 10 salários mínimos é de 0,2.
(III) A proporção de indivíduos que recebem até 20 salários mínimos é de 0,7.
(IV) A proporção de indivíduos casados entre os que recebem mais de 20 salários mínimos é de 0,7.
(V) A proporção de indivíduos que recebem até 10 salários mínimos entre os solteiros é de 0,3. (a) Construa a distribuição conjunta das variáveis estado civil e faixa salarial e as respectivas distribuições marginais.
(b) Você diria que existe relação entre as duas variáveis consideradas?
Passo 1
(a) Construa a distribuição conjunta das variáveis estado civil e faixa salarial e as respectivas distribuições marginais.
Considere:
- X: faixa salarial e
- Y: estado civil
Primeiro, vamos montar a nossa tabela, mas com ela vazia (sem valores), só para termos uma base.
Passo 2
Agora, vamos analisar os dados que o enunciado nos dá:
(I) A proporção de indivíduos solteiros é de 0,4.
Se a proporção total de indivíduos solteiros é de 0,4, ela vai entrar na 2ª linha com a última coluna. E consequentemente a proporção total de indivíduos casados é de 0,6 que vai entrar na 3ª linha com última coluna.
(II) A proporção de indivíduos que recebem até 10 salários mínimos é de 0,2.
Se a proporção total de indivíduos que recebem até 10 salários mínimos é de 0,2, ela vai entrar na última linha linha com a 2ª coluna.
(III) A proporção de indivíduos que recebem até 20 salários mínimos é de 0,7.
Como nós já sabemos que a proporção de indivíduos que recebem até 10 salários mínimos é de 0,2. Logo a proporção total de indivíduos que recebem entre 10 a 20 salários mínimos é de 0,5 (0,7 – 0,2).
(IV) A proporção de indivíduos casados entre os que recebem mais de 20 salários mínimos é de 0,7.
Nessa, precisamos pensar um pouco mais. Nós já sabemos que 0,2 recebem menos de 10 salários mínimos e que 0,5 recebem entre 10 e 20 salários míminos, logo sobram 0,3 [1 –(0,2 + 0,5)] indivíduos que recebem mais de 20 salários mínimos. A proporção de indivíduos casados entre os que recebem mais de 20 salários mínimos é de 0,7, logo dos indivíduos que recebem mais de 20 salários mínimos, 0,21 (0,7 X 0,3) são casados e 0,9 (0,3 – 0,21) são solteiros.
(V) A proporção de indivíduos que recebem até 10 salários mínimos entre os solteiros é de 0,3.
Só seguirmos o mesmo raciocínio do anterior só que de maneira inversa. Nós já sabemos que a proporção total de indivíduos solteiros é de 0,4. Se desses 0,4, 0,3 recebem até 10 salários mínimos, então temos um total de 0,12 (0,3 X 0,4).
Já temos todas as informações necessárias para montarmos a nossa tabela da distribuição conjunta das variáveis estado civil e faixa salarial e as respectivas distribuições marginais.
Completando a tabela, temos
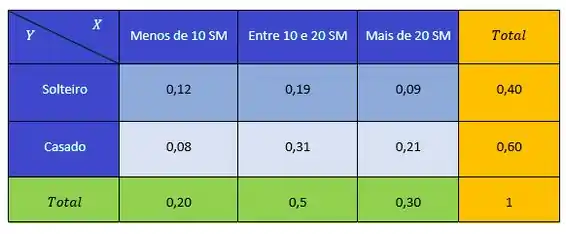
Passo 3
(b) Você diria que existe relação entre as duas variáveis consideradas?
Inicialmente, verificamos que fica muito difícil tirar alguma conclusão, devido à diferença entre os totais marginais. Devemos, pois, construir as proporções segundo as linhas ou as colunas para podermos fazer comparações. Fixemos os totais das colunas
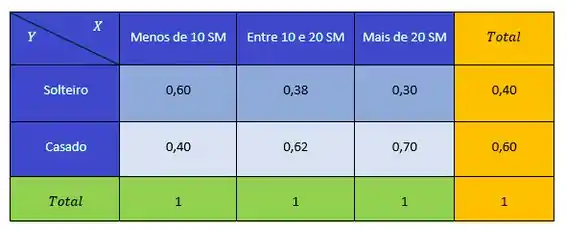
Podemos notar pela tabela de cima que pelas diferenças entre as proporções marginais e as do interior da tabela, parece haver relação entre as variáveis.
Resposta
(a)
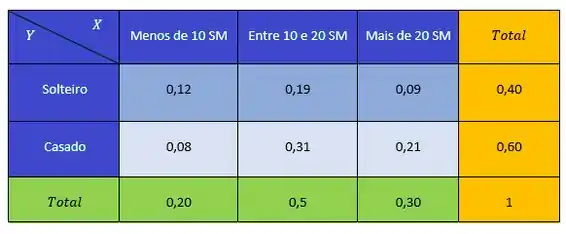
(b) Pelas diferenças entre as proporções marginais e as do interior da tabela, parece haver relação entre as variáveis.