Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 1.2 - Ex. 5
Um estudo pretende verificar se o problema da desnutrição em adultos medida pelo peso, em quilos, em uma região agrícola (denotada por Região A), é maior do que em uma região industrial (Região B). Para tanto, uma amostra foi tomada em cada região, fornecendo a tabela de frequências a seguir:
- Os dados apresentados sugerem que o grau de desnutrição é diferente nas duas regiões? (Note que o total de observações difere em cada região).
- Construa, a partir dos dados das tabelas, um histograma para cada região. Faça uma suposição conveniente para as faixas não delimitadas.
- Com base nos histogramas apresentados em (b), obtenha as medidas necessárias e construa o box-plot, um para cada região. Com base nessa representação gráfica, rediscuta o item (a).
Passo 1
- Vamos calcular as porcentagens relativas a cada classe e reparar que o peso representado em cada tabela são diferentes:
- Vou dividir as classes em uma amplitude de 10, e montar o histograma:
- Construindo os box-plots, para isso vou ter que calcular os quartis ( e para isso vou usar a fórmula de Quartis para dados agrupados:
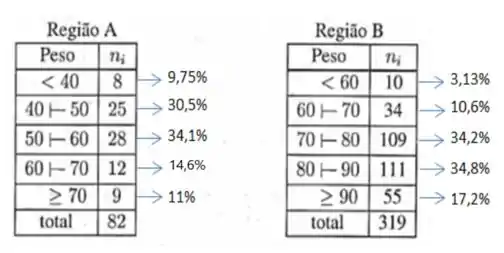
Logo podemos observar que a região B apresenta uma porcentagem mais alta de pessoas mais pesadas e as medidas dos pesos são mais altas. Logo não devemos considerar que o grau de desnutrição seja o mesmo em ambas as regiões.
Passo 2
Região A:
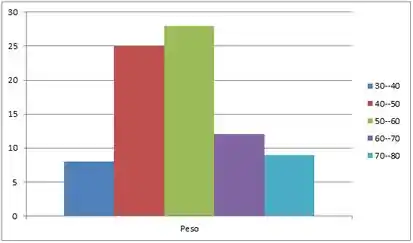
Região B:
Passo 3
- é o quaritl que desejamos calcular, no caso , e
- é o limite inferior da classe que estamos trabalhando
- é a posição que se encontra o valor do nosso quartil
- é a frequência acumulada até a classe que estamos
- é a frequência da classe que estamos trabalhando
- é a amplitude da classe
Passo 2
Região A:
Onde , porque estamos no primeiro quartil e é o numero de pessoas medidas na Região A.
Logo o está na segunda classe, e calculando
Aplicando o mesmo processo para
Logo se encontra na terceira classe:
Aplicando o processo para :
Logo se encontra na quarta classe, porque até a terceira classe acumulamos 58 dados, e a conta a cima nos informa que está na posição 61,5, ou seja, em algum lugar no meio dos 12 dados da quarta classe:
Sendo o mínimo da região A 30 e o máximo 80.
Passo 3
Calculando os mesmo valores, só que para a região B.
está na terceira classe:
está na quarta classe:
também está na quarta classe:
Na região B temos que o mínimo é 50 e o máximo é 100
Passo 4
Construindo os box-plot:
Então nossas suspeitas estavam corretas, e realmente nos parece que a Região A é uma região subnutrida em relação a B.
Resposta
Ei, a resposta está no passo a passo :)