No Exercicio 6-45,dados foram apresentados sobre o tempo de ignicao fria de uma gasolina particular usada em um veiculo de teste. Uma segunda formulacao da gasolina foi testada no mesmo veiculo.com os seguintes tempos(em segundos): 1,83, 1,99, 3,13, 3,29, 2,65, 2,87, 3.40, 2.46, 1.89 e 3.35.Use esses novos dados.juntamente com os tempos de ignicao fria reportados no Exereicio 6-45 para construir diagramas de caixa comparativos. Escreva uma interpretacaio da informacio que voce ve nesses diagramas.

Novos dados:

Ordene os valores dos dados do menor para o maior:

1.83, 1.89, 1.99, 2.46, 2.65, 2.87, 3.13, 3.29, 3.35, 3.4

Como o número de pontuações é par, a mediana é a média dos dois valores intermediários do conjunto de dados classificado:

O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):

O terceiro quartil é a mediana dos valores dos dados acima da mediana (ou em 75% dos dados):

Os bigodes do boxplot estão no valor mínimo e máximo. A caixa começa no quartil inferior, termina no quartil superior e tem uma linha vertical na mediana.

O quartil inferior está em 25% da lista de dados classificados, a mediana em 50% e o quartil superior em 75%.

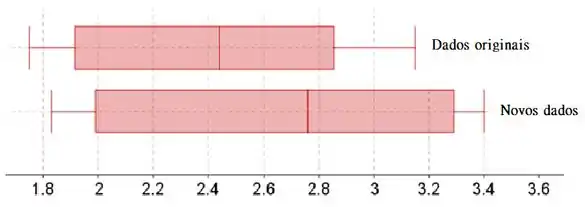
Ambos os conjuntos de dados parecem não ter outliers.

Ambas as distribuições parecem ser aproximadamente simétricas.

O centro (mediana) para os novos dados é mais alto do que o centro para os dados originais, porque a linha vertical na caixa do boxplot está mais à direita para os novos dados.

O spread para os novos dados é maior do que o spread para os dados originais, porque a largura entre os bigodes é maior para os novos dados.