Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 7.Exercícios - Ex. 40
O Exercício 13 do Capítulo 1 apresentou uma amostra de observações sobre a resistência à tensão máxima, e o Exercício 17 da seção anterior forneceu quantidades resumidas e pediu o intervalo de confiança de amostra grande. Em virtude de o tamanho da amostra ser grande, nenhuma suposição sobre a distribuição da população é necessária para a validade do IC.
a. Qualquer suposição sobre a distribuição da resistência à tensão é necessária, antes de calcular um limite de previsão inferior para a resistência à tensão do próximo espécime selecionado usando o método descrito nesta seção? Explique.
b. Use um programa estatístico para investigar a plausibilidade de uma distribuição normal da população.
c. Calcule o limite de previsão inferior com um nível de previsão de para a resistência extrema à tensão do próximo espécime selecionado.
Passo 1
a. Precisamos assumir que as amostras vieram de uma população normalmente distribuída.
Passo 2
b. Um gráfico de probabilidade normal, gerado pelo Minitab:
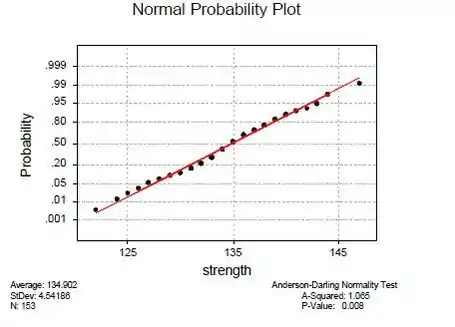
O valor de p muito pequeno indica que a distribuição populacional da qual esses dados foram obtidos provavelmente não é normal.
Passo 3
c. Limite de previsão inferior de 95 %:
Resposta
Precisamos assumir que as amostras vieram de uma população normalmente distribuída.
b. O valor de p muito pequeno indica que a distribuição populacional da qual esses dados foram obtidos provavelmente não é normal.
c.