Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 6.Exercícios Suplementares - Ex. 35
Seja a amostra aleatória de uma fdp que seja simétrica com relação a . Um estimador de considerado por realizar bem uma variedade de distribuições subjacentes é o estimador de Hodges-Lehmann. Para defini-lo, calcule primeiro para cada e cada , 2, ..., a média de pareados . Então, o estimador é a mediana dos s. Calcule o valor dessa estimativa, usando os dados do Exercício 44, do Capítulo 1. (Sugestão: construa uma tabela quadrada com os listados na margem esquerda e na parte superior. Depois, calcule as médias na diagonal e acima dela.)
Passo 1
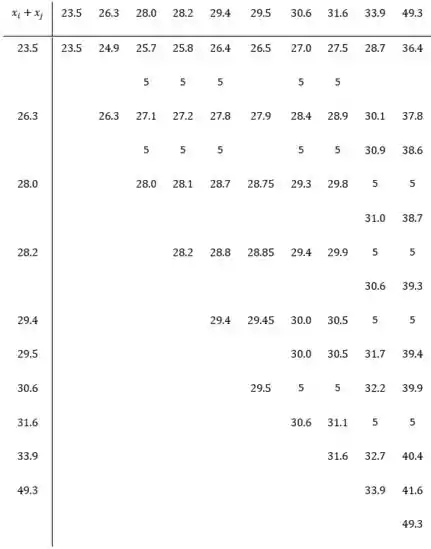
Existem 55 médias, então a mediana é o 28th em ordem crescente de magnitude. Portanto,
Resposta
Exercícios de Livros Relacionados
Considere as observações que seguem sobre o fluxo direto (1000 acre-pés) registrado em um posto em Colorado de 12 de abril a 31 de agosto, por um período de 31 anos (Dados extraídos de um artigo do vo
Em uma amostra aleatória de certo tipo de 80 componentes, 12 são considerados defeituosos.a. Forneça uma estimativa pontual da proporção de todos os componentes que nāo são defeituosos.b. Um sistema s
Suponha que certo tipo de fertilizante possua um rendimento esperado por acre de μ 1 , com variância σ 2 , enquanto o rendimento esperado de um segundo tipo de fertilizante seja μ 2 com a mesma variân
Considere a seguinte amostra de observações sobre a espessura da camada da pintura de baixa viscosidade ("Achieving a Target Value for a Manufacturing Process:A Case Study," J. of Quality Technology,
Seja X 1 , X 2 , … , X n uma amostra aleatória de uma fdp f ( x ) simétrica em relação a μ , de modo que X ˜ seja um estimador não-tendencioso de μ . Se n for grande, pode-se mostrar que V ( X ˜ ) = 1