Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 90
Em um experimento para estudar a relação entre hipertensão e o hábito de fumar, os seguintes dados foram obtidos de 180 indivíduos
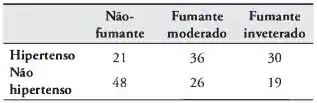
Teste a hipótese de que a presença ou ausência da hipertensão depende dos hábitos relacionados ao fumo. Use um nível de significância de 0,05.
Passo 1
Oii pessoal, show de bola??
“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”
Bora empurrar e macetar essa questãozinha comigo agora
Testar
O nível de significância especificado é .
Vamos seguir a tabela seguinte
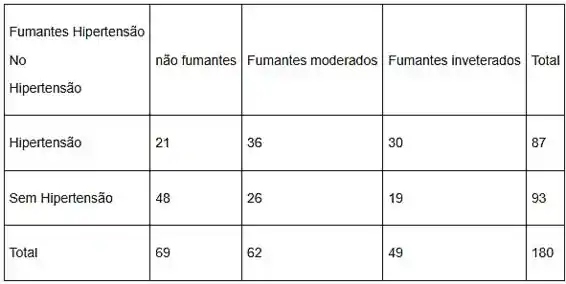
Passo 2
A regra geral para obtenção da frequência esperada de qualquer célula é dada pela seguinte expressão
Na tabela a seguir, mostraremos a frequência observada junto com a frequência esperada ente colchetes para cada célula
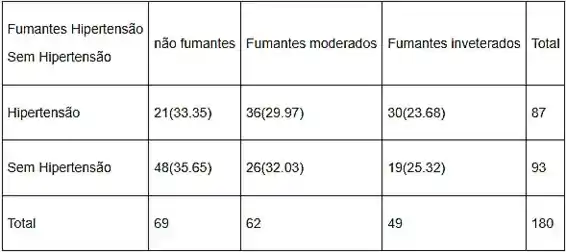
Passo 3
A estatística do teste qui-quadrado é dada como
Sob a estatística de teste segue a distribuição de com graus de liberdade, pois há duas linhas e três colunas.
A região crítica é dada como onde é o ponto 0.05 superior da distribuição com 2 graus de liberdade.
Portanto, rejeite e conclua que fumar e hipertensão não é independente.
“Faça seus medos terem medo de você”
Resposta
Portanto, rejeite e conclua que fumar e hipertensão não é independente.