Em um estudo conduzido no Instituto Politécnico e Universidade Estadual da Virgínia, os níveis de ácido ascórbico no plasma de mulheres grávidas foram comparados entre as fumantes e as não-fumantes. Trinta e duas mulheres, nos três últimos meses de gravidez, livres da maioria das doenças e com idades entre 15 e 32 anos, foram selecionadas para o estudo. Antes da coleta de 20 ml de sangue, as mulheres evitaram café da manhã, abriram mão das vitaminas e evitaram alimentos com alta concentração de ácido ascórbico. Nas amostras de sangue, foram determinados os valores de ácido ascórbico no sangue de cada uma, em miligramas por 100 mililitros:
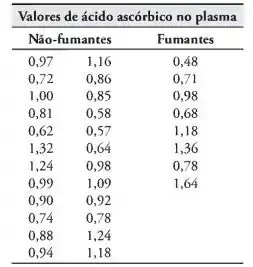
Há evidências suficientes para concluirmos que há uma diferença entre os níveis de ácido ascórbico no plasma das fumantes e não-fumantes? Assuma que os dois conjuntos de dados vêm de populações normais com variâncias desiguais. Use um valor P
Passo 1
Falaaaa moçadinha, show de bola?
Como diz o Homem de ferro “Eu tenho um plano. Ataque!”

Bora atacar esse problemaaaaaaa junto comigoo.
O objetivo do estudo é testar a alegação de que existe uma diferença entre os níveis plasmáticos de ácido ascórbico de fumantes e não fumantes.
Sejam , respectivamente, as verdadeiras médias populacionais para o nível plasmático de ácido ascórbico de fumantes e não fumantes.
Para testar
Vamos considerar o nível de significância
A estatística de teste é a seguinte
Onde
média amostral do nível plasmático de ácido ascórbico de mulheres fumantes
média amostral do nível plasmático de ácido ascórbico de mulheres não fumantes
tamanho da amostra para nível plasmático de ácido ascórbico de mulheres fumantes
tamanho da amostra para o nível plasmático de ácido ascórbico de mulheres não fumantes
= diferença entre as médias populacionais sob
= variância da amostra para nível de ácido ascórbico plasmático de mulheres fumantes
= variância da amostra para o nível plasmático de ácido ascórbico de mulheres não fumantes
Sob , a estatística de teste segue t-distribuição com v graus de liberdade onde
Passo 2
Vamos considerar a tabela a seguir

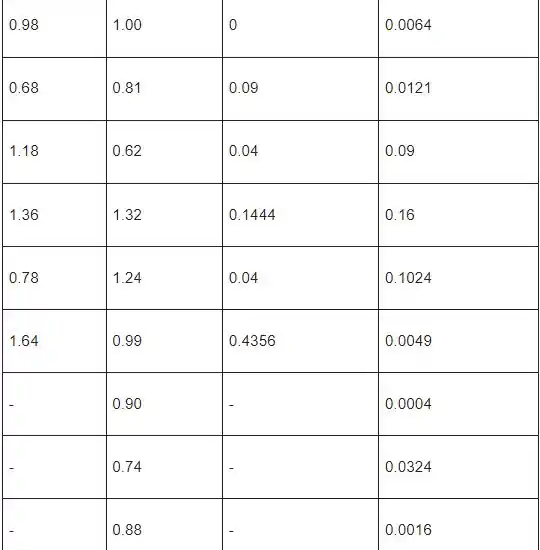
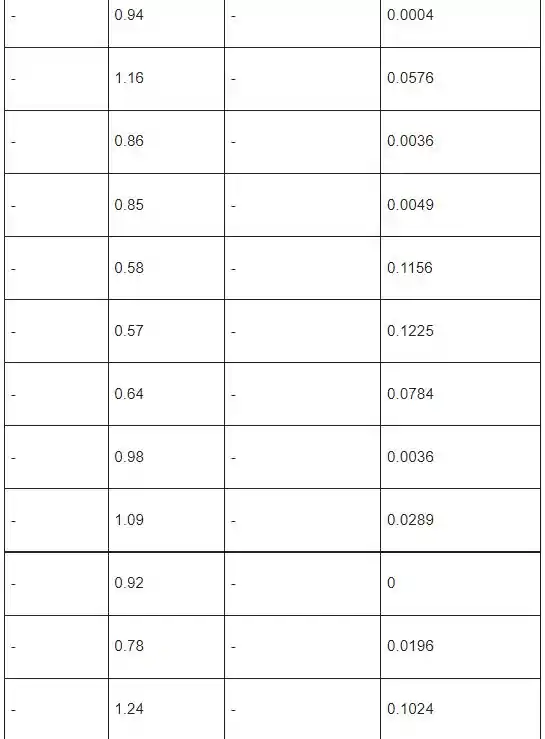
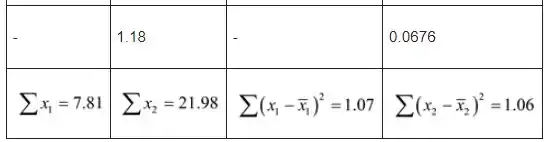
Passo 3
Passo 4
Em seguida, iremos o valor da estatística de teste da seguinte maneira
O valor da estatística de teste é de
Passo 5
Vamos determinar os graus de liberdade
Regra de decisão:
Rejeitar
Das tabelas t com nível de significância de 5% com 8 graus de liberdade, o valor crítico bicaudal
é,
Observa-se claramente que o valor de , que é menor que o valor crítico de Assim, falhe em rejeitar a hipótese nula a um nível de significância de 5%.
Não há evidências suficientes para concluir que existe uma diferença entre o nível plasmático de ácido ascórbico de fumantes e não fumantes.
“Às vezes é preciso aprender a correr antes de começar a andar”

Resposta
Não há evidências suficientes para concluir que existe uma diferença entre o nível plasmático de ácido ascórbico de fumantes e não fumantes.