Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 3.1 - Ex. 51
Experimento probabilístico
Nos exercícios 51 a 54, um experimento probabilístico consiste em lançar um dado de seis faces e rodar o disco mostrado a seguir. O disco apresenta a mesma chance de parar sobre cada cor. Use um diagrama de árvore para encontrar a probabilidade do evento e, em seguida, diga se o evento pode ser considerado incomum.
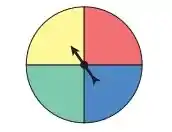
Evento A: sair face 5 e cor azul.
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
No caso, nós temos aqui duas situações acontecendo:
O Evento consiste de cair a face 5 no dado e a cor azul no disco. Vamos calcular a probabilidade individual primeiro.
Começando pela probabilidade de tirar face 5 no dado. Como só há 1 face 5 num dado de 6 faces, a probabilidade:
Agora pro disco. Como só há 1 quadrante com a cor azul, a probabilidade vai ser:
Como nós queremos a probabilidade de cair a face 5 sair a cor azul, nós vamos multiplicar:
A probabilidade do Evento A é de 0,42.