Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 7.3 - Ex. 2
O número de divórcios por indivíduo adulto casado, em certa comunidade, foi modelado pela variável aleatória , cuja função de probabilidade é apresentada a seguir.
Uma amostra, representada por foi sorteada com dois desses indivíduos e os seguintes estimadores, para média de divórcios, foram considerados: e máximo – mínimo. Para cada estimador, obtenha sua distribuição de probabilidade e verifique se é viciado.
Passo 1
Oi, tudo bem? Bora resolver mais um exercício? Vamos construir uma tabela para distribuição de probabilidade de :
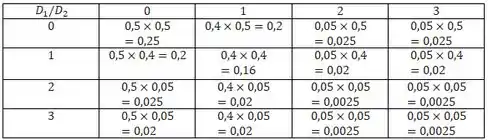
Assim,
;
;
Para este estimador, temos a esperança:
Passo 2
Vamos lá! Vamos agora construir uma tabela para a distribuição de máximo – mínimo:
Observação: o valor entre parênteses representa a probabilidade de ocorrência. Dessa forma, podemos então obter a distribuição de probabilidade do estimador:
Para este estimador, temos a esperança:
Passo 3
Vamos lá, para verificar se estes estimadores são viciados, vamos calcular a esperança da população:
Como os valores das esperanças de ambos os estimadores diferem do valor da esperança da população, concluímos que eles são viciados.
Resposta
Assim, concluímos que ambos os estimadores são viciados.