Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 12.Exercícios propostos - Ex. 3
Quatro analistas determinam o rendimento de dado processo. Por comodidade, oitenta unidades foram subtraídas dos dados originais a fim de dar a seguinte tabela de valores:
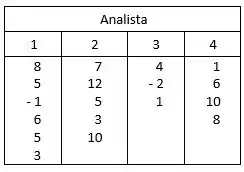
Pede-se:
- Diferem os analistas significativamente em suas determinações de rendimento, com ?;
- Teria a conclusão do item anterior sido diferente se as oitenta unidades não houvessem sido subtraídas na apresentação dos dados?
Passo 1
Olá galerinha, vamos lembrar um pouquinho sobre análise de variância? Vem comigo!
A análise de variância constitui-se de um conjunto de técnicas estatísticas para descobrir “fatores” que produzem mudanças sistemáticas em alguma variável de interesse. Os fatores propostos podem ser variáveis quantitativas ou qualitativas, enquanto a variável dependente é quantitativa e é observada dentro das classes dos fatores.
Sabendo disso, vamos lá!
- Definir as hipóteses nula e alternativa:
- :
- : pelo menos uma diferente
Onde:
- n° de tratamentos
- n° total de elementos
Então:
Passo 2
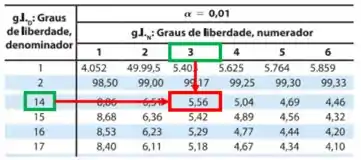
Onde:
Temos o seguinte:
Então primeiramente iremos calcular o valor :
A variação entre amostras é:
A variação total:
E com esses valores, conseguimos encontrar a variação dentro da amostra:
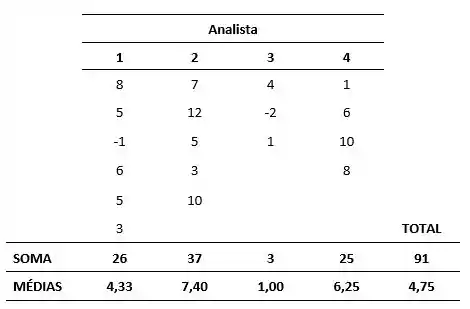
Sendo assim, conseguimos completar nossa tabela:
Para o item a), concluímos que para , os analistas não diferem significativamente em suas determinações de rendimento.
Passo 3
b) A conclusão poderia ser diferente, se as oitentas unidades não houvessem sido subtraídas na apresentação dos dados, porque o tamanho da amostra é relevante para o teste estatístico, pois sabemos que quanto maior o tamanho da amostra, maior o poder do teste.
Prontinho pessoal, até mais!
Resposta
- aceitamos , os analistas não diferem.
- A conclusão poderia ser diferente.