Reconsidere os dados de velocidade do semicondutor do Exercício 6-26. Construa um diagrama de caixa dos dados e escreva uma interpretação do gráfico. Como o diagrama de caixa se compara, em valor interpretativo, ao diagrama original de ramo e folhas?

Como o número de pontuações é par, a mediana é a média dos dois valores médios do conjunto de dados classificado:

O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):

O terceiro quartil é a mediana dos valores de dados acima da mediana (ou em 75% dos dados):

Os bigodes do diagrama de caixa estão no valor mínimo e máximo. A caixa começa no quartil inferior, termina no quartil superior e tem uma linha na mediana.

O quartil inferior está em 25% da lista de dados classificados, a mediana em 50% e o quartil superior em 75%.

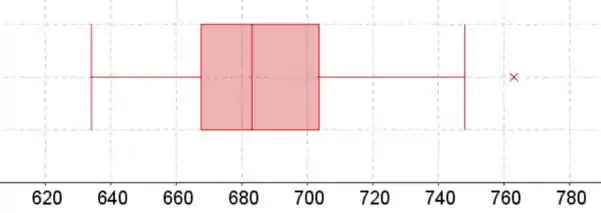
O diagrama de caixa oferece um valor interpretativo tão bom quanto o de ramo e folha original, porque observamos o mesmo outlier no diagrama de caixa e a distribuição parece estar aproximadamente simétrica em ambas as imagens .

O diagrama de ramo e folha também nos permite determinar os valores dos dados do conjunto de dados e os percentis da distribuição, o que não é possível com o diagrama de caixa.