As nove medidas que seguem são temperaturas de fornalha registradas em batelada de sucessivas de um processo de fabricação de semicondutores (unidades em): calcule a média, variância desvio padrão da mostra. Encontre a mediana. Quanto maior a medida de temperatura poderia aumentar sem mudar o valor da mediana? Construam diagrama de caixa de dados.
Passo 1
Letra a:
A média é a soma de todos os valores dividida pelo número de valores:
n é o número de valores no conjunto de dados.
A variância é a soma dos desvios quadrados da média dividida por :
O desvio padrão é a raiz quadrada da variância:
Passo 2
Letra b:
Ordene os valores dos dados do menor para o maior:
948, 949, 950, 951, 953, 954, 955, 955, 957
Como o número de pontuações é ímpar, a mediana é o valor médio do conjunto de dados classificado:
Não há limite para o qual a medição de temperatura mais alta pode aumentar sem alterar o valor da mediana, porque o valor do meio não é afetado pelo maior valor no conjunto de dados.
Passo 3
O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):
O terceiro quartil é a mediana dos valores de dados acima da mediana (ou em 75% dos dados):
Passo 4
Os bigodes do boxplot estão no valor mínimo e máximo. A caixa começa no quartil inferior, termina no quartil superior e tem uma linha na mediana.
O quartil inferior está em 25% da lista de dados classificados, a mediana em 50% e o quartil superior em 75%.
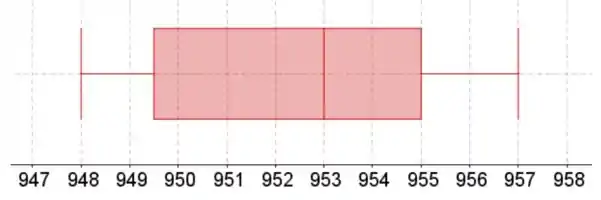
Resposta
- Média: 952.444
- Mediana: 953
- Veja o boxplot
Variancia: 9.53
Desvio-padrão: 3.0867
Sem limite