Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 7.Exercícios - Ex. 9
Suponha que X tem um Distribuição discreta uniforme
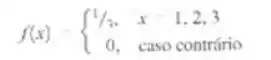
Uma amostra aleatória de N = a 36 e selecionada dessa população. Encontre a probabilidade da média amostral ser maior do que 2,1, porém menor do que 2,5, considerando que a média amostral seja medida com precisão na primeira casa decimal.
Passo 1
A variável aleatória X segue uma distribuição uniforme discreta
O exercício nos dá e
Portanto,
A média da amostra é:
e desvio padrão:
Passo 2
Vamos encontrar a probabilidade de que a média da amostra esteja entre 2.1 e 2.5:
Resposta
0.232574
Exercícios de Livros Relacionados
Nos exercícios 17 a 34, encontre a média, a mediana e a moda dos dados, se possível. Se quaisquer dessas medidas não puderem ser encontradas ou não representarem o centro dos dados, explique o porquê.
Nos exercícios 17 a 34, encontre a média, a mediana e a moda dos dados, se possível. Se quaisquer dessas medidas não puderem ser encontradas ou não representarem o centro dos dados, explique o porquê.
Nos exercícios de 37 a 40, sem realizar nenhum cálculo, determine qual medida de tendência central melhor representa os dados dos gráficos a seguir. Explique seu raciocínio39. Frequências cardíacas de
Nos exercícios 17 a 34, encontre a média, a mediana e a moda dos dados, se possível. Se quaisquer dessas medidas não puderem ser encontradas ou não representarem o centro dos dados, explique o porquê.
Construindo conjuntos de dados - Nos exercícios 5 a 8, construa o conjunto de dados descrito. Os valores no conjunto de dados não podem ser os mesmos.6. A média e a moda são as mesmas.