Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 6.Exercícios - Ex. 84
Os seguintes dados são as temperaturas de fluente em dias consecutivos na descarga de uma estação de tratamento de esgoto:
- Calcule a média, mediana, a variância e o desvio padrão da mostra.
- Construa um diagrama encaixa dos dados e comente a informação obtida nesse diagrama.
Passo 1
Letra a:
A média é a soma de todos os valores dividida pelo número de valores:
n é o número de valores no conjunto de dados.
Vamos ordenar os valores dos dados do menor para o maior:
Já que o número de valores é par, a mediana é a média dos dois valores médios do conjunto de dados classificado:
A variância da amostra é a soma dos desvios quadrados da média dividida por :
O desvio padrão da amostra é a raiz quadrada da variância:
Passo 2
Letra b:
O primeiro quartil é a mediana dos valores de dados abaixo da mediana (ou em 25% dos dados):
O terceiro quartil é a mediana dos valores de dados acima da mediana (ou em 75% dos dados):
Os whiskers (bigodes) do boxplot estão no valor mínimo e máximo. A caixa começa no quartil inferior, termina no quartil superior e tem um linha na mediana.
O quartil inferior está em 25% da lista de dados classificados, a mediana em 50% e o quartil superior em 75%.
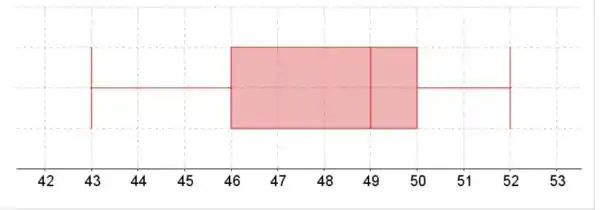
A distribuição parece estar ligeiramente inclinada para a esquerda, porque a caixa parece estar à direita entre os whiskers e a linha vertical dentro da caixa do boxplot parece estar à direita da caixa.
Resposta
- Média 48.125, Mediana 49, Variância 7.25, Desvio padrão 2.9616
- A distribuição parece estar ligeiramente inclinada para a esquerda, porque a caixa parece estar à direita entre os whiskers e a linha vertical dentro da caixa do boxplot parece estar à direita da caixa.