Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 10.Problemas - Ex. 38d
Suponha que temos a população ). Gere amostras de tamanho dessa população, usando algum programa de geração de valores de uma distribuição normal, como o Excel ou Minitab.
(d) Estude a distribuição da estatística “variância da amostra”.
Passo 1
Vamos construir os gráficos para a “variância da amostra”: Histograma
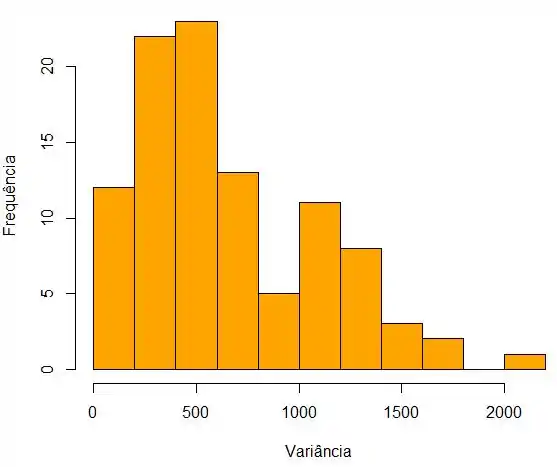
Passo 2
Boxplot:
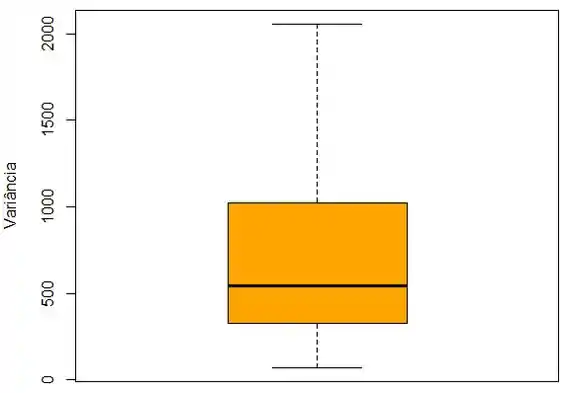
Passo 3
Ramos-e-folhas:
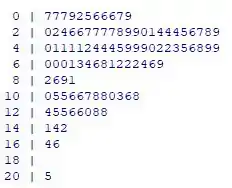
Resposta
Medidas-Resumo:
Exercícios de Livros Relacionados
Suponha uma população P={ 1 ,2 , . . . ,N } e a v.a. X definida sobreP . Então, T = ∑ i = 1 N X i é chamado total populacional. A média populacional é μ=T / N e a variância populacional é σ 2 = ∑ i =
Compare o valor de P ( X ≥ 1 ) , onde tem distribuição, N ( 0,1 ) , com P t ≥ 1 , onde t tem distribuição t de Student com: a) 5gl., b) 10gl., c) 15gl., d) 20gl, e) 25gl.
Testou-se um componente que se supõe ter uma distribuição de falhas exponencial. Foram observadas as seguintes durações de vida (em horas); 108, 212, 174, 130, 198, 169, 252, 168, 143. Empregando esse
Suponha que X tenha uma distribuição de Weibull, com fdp f x = λ α x α - 1 e - λ x α ,x0 Suponha que α seja conhecido. Determine a estimativa MV de λ , baseada em uma amostra de tamanho n.
Uma variável aleatória X tem distribuição N ( μ , 1 ) . Tomam-se vinte observações de , mas em vez de se registrar o valor real, somente anotamos se X era ou não era negativo. Suponha que o evento {X