Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 50

Suponha que X e Y tenham a seguinte distribuição de probabilidade conjunta:

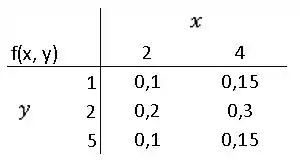
(a) Determine a distribuição marginal de X.

(b) Determine a distribuição marginal de Y.

Passo 1

Falaa, meu querido/minha querida. Como a distribuição de probabilidade conjunta é fornecida com a tabela, encontraremos a distribuição marginal das variáveis em cada valor lendo a tabela e inserindo esses valores lidos na fórmula. Então, bora finalizar a questão!!!

Passo 2

Para a variável aleatória X , nós temos:

g 2 = ∑ y f 2 ,   y = f 2 ,   1 + f 2 ,   3 + f 2 ,   5 = 0,1 + 0,2 + 0,1 = 0,4

g 4 = ∑ y f 4 ,   y = f 4 ,   1 + f 4 ,   3 + f 4 ,   5 = 0,1 5 + 0 , 3 + 0 , 15 = 0 , 6

Passo 3

Para a variável aleatória Y , temos:

h 1 = ∑ x f x ,   1 = f 2 ,   1 + f 4 ,   1 = 0,1 + 0,15 = 0,25

h 3 = ∑ x f x ,   3 = f 2 ,   3 + f 4 ,   3 = 0 , 2 + 0 , 3 = 0 , 5

h 5 = ∑ x f x ,   5 = f 2 ,   5 + f 4 ,   5 = 0,1 + 0,15 = 0,25

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

A urna I contém 2 bolas brancas e 4 bolas vermelhas, enquanto a urna II contém 1 bola branca e 1 bola vermelha. Uma bola é aleatoriamente escolhida da urna I e colocada na urna II, e então uma bola é
Cinquenta e dois por cento dos estudantes de certa faculdade são mulheres. Cinco por cento dos estudantes desta faculdade estão se formando em ciência da computação. Dois por cento dos estudantes são
Considere duas caixas, uma contendo 1 bola de gude branca e 1 branca, e a outra contendo 2 bolas de gude brancas e 1 branca. Uma caixa é selecionada aleatoriamente e uma bola de gude é retirada de for
Noventa e oito por cento de todas as crianças sobrevivem ao parto. Entretanto, 15% de todos os nascimentos envolvem cesarianas ( C ) , e quando uma cesariana é feita os bebês sobrevivem em 96 % dos ca
No Exemplo 3a, qual é a probabilidade de que alguém sofra um acidente no segundo ano dado que ele ou ela não tenha sofrido acidentes no primeiro ano?