Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 20

A tabela a seguir representa a função de probabilidade conjunta de duas variáveis aleatórias independentes.

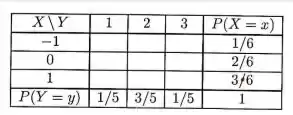
  1. Complete a tabela.
  2. Determine E X ,   E Y   e   C o v ( X , Y ) .
  3. Calcule V a r X + Y .

Passo 1

Vamos completar a tabela de dupla entrada. Como as variáveis são independentes, podemos pegar o produto das marginais referentes ao campo desejado pra preencher a tabela, da seguinte maneira:

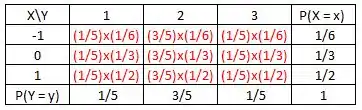
Assim, teremos:

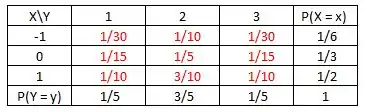
Passo 2

Em (b) vamos calcular a esperança e a covariância das variáveis. Temos que a esperança é dada por:

E X = ∑ x ⋅ p ( x )   o u   E Y = ∑ y ⋅ p ( y )  

Assim,

E X = - 1 6 + 1 2 = 2 6 = 1 3

E Y = 1 5 + 6 5 + 3 5 = 10 5 = 2

Já a covariância, é dada pela seguinte expressão:

C o v X , Y = E X Y - E X E ( Y )

Vamos montar a tabela de XY e sua função de probabilidade, assim:

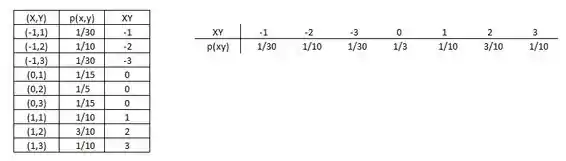
Daí,

E X Y = - 1 30 - 2 10 - 1 10 + 1 10 + 3 10 + 1 10 = 1 6

Logo,

C o v X , Y = 1 6 - 2 3 = - 1 2

Passo 3

Temos em (c) que a variância da soma será dada por:

V a r X + Y = V a r X + V a r Y

Também temos que:

V a r X = E X 2 - E X 2

Assim,

V a r X = 1 6 + 1 2 - 1 3 2 = 5 9

V a r Y = 1 5 + 12 5 + 9 5 - 4 = 2 5

Daí,

V a r X + Y = 5 9 + 2 5 = 0,95

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se X tiver distribuição de X_n ² ², mostre que E (X) = n e V (X) = 2 n
Determine a fgm da tensão (incluindo o ruído) tal como apresentada no Probl. 7.25 e obtenha o valor esperado e a variância dessa tensão.
Suponha que a variável aleatória X tenha fdp. f X = 1 2 e - x ,- ∞x+ ∞ Determine a fgm de X, ache E(X) e V(X).
Suponha que X tenha a seguinte fdp: f x = λ e - λ x - a ,x ≥ a Determine a fgm de X, ache E(X) e V(X).
Suponha que V, a velocidade (cm/seg) de um objeto, tenha distribuição N ( 0,4 ) . Se K = m V 2 2 for a energia cinética do objeto (onde m=massa), determine a fdp de K. Se m=10g, calcule P ( K ≤ 3 ) .