Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 10.Exercícios propostos - Ex. 13

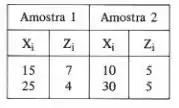
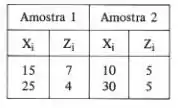
Testar a significância da igualdade entre as médias populacionais das duas amostras abaixo, para 5 %     e     1 % , supondo os dois casos: σ 1 = σ 2     e     σ 1 ≠ σ 2 .

a)

b)

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão ele pede para testar a significância das igualdades entre as médias populacionais das amostras abaixo para 5 %     e     1 % . Supondo os casos: σ 1 = σ 2     e     σ 1 ≠ σ 2 .

a)

b)

Passo 2

Na letra (a) sabendo que,

0,5 % → 0,05 → Z α 2 = 1,96

0,1 % → 0,01 → Z α 2 = 2,576

H 0 = u 1 = u 2 H 1 = u 1 ≠ u 2

Amostra 1: Amostra 2:

∑ = 8 ∑ = 9  

α = 8 3 = 2,667 α = 9 3 = 3

s d 2 = 1 4 ( 24 - 3.2,67 2 ) s d 2 = 1 4 30 - 3 . 3 2 = 0,75

s d = 0,81 s d = 0,87

t = 2,67 - 10 0,81 5 = - 0,32 t = 3 - 10 0,8 7 1 = - 0,32

- 0,32 em ambos os casos

Passo 3

Na letra (b),

0,5 % → 0,05 → Z α 2 = 1,96

0,1 % → 0,01 → Z α 2 = 2,576

H 0 = u 1 = u 2 H 1 = u 1 ≠ u 2

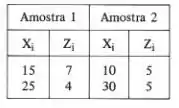
Amostra 1: Amostra 2:

∑ = 11   ∑ = 10

α = 11 2 = 5,5 α = 10 2 = 5

s d 2 = 1 4 ( 40 - 2 . 5,5 2 ) s d 2 = 1 4 40 - 2.5 2

s d = 2,26                                                                                                                                                       s d = 1,58                                          

t = 2,67 - 10 2,26 5 = - 0,88 t = 1,58 - 10 1,58 1 = - 0,3 7

De boa né? espero ter ajudado blz.

Resposta

a) - 0,32 em ambos os casos

b) t = - 0,88     e   t = - 0,37

Exercícios de Livros Relacionados

Num levantamento de opinião pública para previsão de uma eleição, foram ouvidos 500 eleitores escolhidos ao acaso; 236 declararam que iriam votar no candidato A e os demais no candidato B. verificar-s
De acordo com reportagens publicadas, a prática sob condições de fadiga distorce os mecanismos que governam o desempenho. Um experimento foi conduzido, utilizando 15 estudantes universitários do sexo
Considere a situação do Exercício 10.54. O consumo de oxigênio em m l / k g / m i n também foi medido nos nove indivíduos:Supõe-se que o consumo de oxigênio deveria ser maior em ambientes relativament
Em um estudo conduzido pelo Departamento de Nutrição Humana e Alimentos da Universidade da Virgínia, foram registrados os dados de comparação dos resíduos de ácido sórbico, em partes por milhão, em pr
Cinco amostras de uma substância ferrosa serão usadas para determinar se há uma diferença no conteúdo de ferro entre uma análise química laboratorial e uma análise com raios X fluorescentes. Cada amos