Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 42
Cinco amostras de uma substância ferrosa serão usadas para determinar se há uma diferença no conteúdo de ferro entre uma análise química laboratorial e uma análise com raios X fluorescentes. Cada amostra foi dividida em duas subamostras e os dois tipos de análises
foram aplicados. A seguir, temos os dados codificados que mostram as análises dos conteúdos
de ferro.
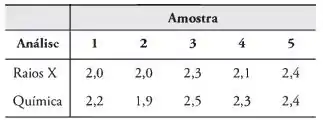
Assumindo que as populações são normais, teste a um nível de significância de 0,05 se os dois testes fornecem, em média, os mesmos resultados.
Passo 1
Falaiii meus amores, cêis tão suave?
“Se alguma coisa está dificil de ser feita, é porque não é para ser feita" # sóquenão”
A partir das informações fornecidas,
Número de substâncias do tipo ferroso
Let são a verdadeira média da população para química de laboratório e análise de fluorescência de raios-X.
Nível de significância .
Enuncie a hipótese nula e alternativa.
Passo 2
Usando a seguinte fórmula para calcular a estatística de teste
Onde
é a média amostral das diferenças entre as observações pareadas
é a diferença entre as médias populacionais sob hipótese nula
é o desvio padrão amostral das diferenças entre as observações pareadas.
Vamos usar a seguinte tabela para os cálculos
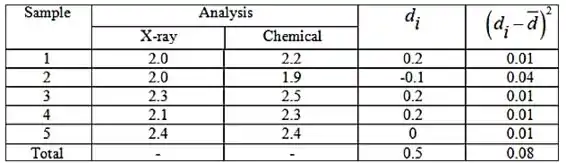
Passo 3
Usaremos as seguintes fórmulas para calcular a média amostral e o desvio padrão da amostra
Passo 4
Agora iremos substituir os valores na fórmula
Portanto, o valor da estatística de teste é de 1.58
O valor critico :
Portanto, o valor crítico é de
Passo 5
Regra de decisão:
Rejeite a hipótese nula, se o valor da estatística de teste for menor que ou maior que
Conclusão:
Isso , significa que o valor da estatística de teste não cai na região crítica.
Assim, não se rejeita a hipótese nula e conclui-se que os dois métodos de análise dão, em média, o mesmo resultado.
Certo, cérebro, eu não gosto de você e nem você de mim, então faça tudo certo pelo menos uma vez para que eu possa continuar te matando com estudos, certo?
Resposta
Resposta nos passos.