Transformações.Em alguns conjuntos de dados,uma transformação por alguma função matemática aplicada aos dados originais,tais como Vy ou log(y).pode resultar em dados que sejam mais fáceis de trabalhar estatisticamente do que os dados originais.Para ilustrar o efeito de uma transformação.considere os seguintes dados,que representam ciclos de falhas de um tecido:675:3650:175:1150:290:2000:100:375.
- Construa um diagrama de caixa e comente a forma da distribuição dos dados.
- Transforme os dados usando logaritmos:isto e.seja y*(novo valor)=log(y)(valor antigo).Construa um grafico de probabilidade normal dos dados transformados e comente o efeito da transtormacao.
Passo 1
Letra a:
Os dados fornecidos estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são as pontuações z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde ao menor valor de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
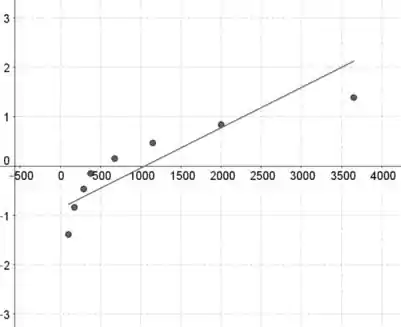
As distribuições de dados parecem não ser aproximadamente normal, porque o padrão nos gráficos de probabilidade normal é fortemente curvado.
Passo 2
Letra b:
Determine os logaritmos de todos os dados:
2.82930377283103, 3.56229286445648, 2.241303804186863, 3.060697840351362 2.46239799789896, 3.301029995661398, 2.00000000000000, 2.57403126772772
Os dados fornecidos estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são as pontuações z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde ao menor valor de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
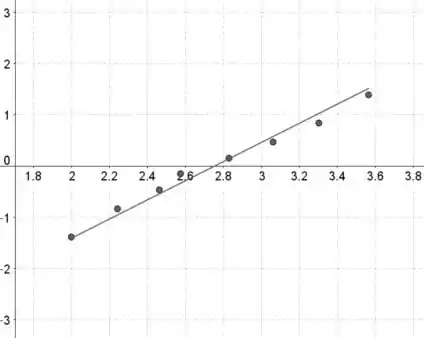
A distribuição de dados parece ser aproximadamente normal, porque o padrão nos gráficos de probabilidade normal é aproximadamente linear.
Resposta
- A distribuição de dados parece não ser aproximadamente normal.
- A distribuição de dados parece ser aproximadamente normal.