Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 10.Problemas - Ex. 2d

Numa urna têm-se cinco tiras de papel, numeradas 1, 3, 5, 5, 7. Uma tira é sorteada e recolocada na urna; então, uma segunda tira é sorteada. Sejam X1 e X2 o primeiro e o segundo números sorteados. Como seriam as respostas anteriores se a primeira tira de papel não fosse devolvida à urna antes da segunda extração?

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para dizer quais as médias e variâncias. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser pensar que, se não tiver reposição, nosso novo espaço amostral será:

{ 13,15,15,17,31,35,35,37,51,53,55,57,51,53,55,57,71,73,75,75 }

Então, nossa tabela fica assim:

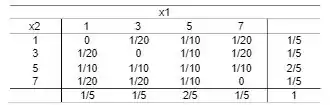
Contudo, podemoss concluir que não são independentes.

Passo 3

Pronto!! Agora, só calcular as médias e variâncias!!

E X 1 = 4,2

E X 2 = 4,2

E X =   E X 1 / 2 + E X 2 / 2 = 4,2

E X ² = 19,2

V a r X = 1,56

Resposta

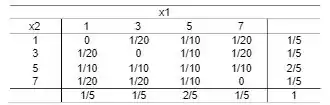
Contudo, podemoss concluir que não são independentes.

E X ² = 19,2

V a r X = 1,56

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para estimar a média das alturas (em metros) numa certa população, dois institutos de pesquisa coletaram cada um a sua amostra e usaram estimadores diferentes. Os resultados estão na tabela abaixo:Voc
Para estimar a média das alturas (em metros) numa certa população, dois institutos de pesquisa coletaram cada um a sua amostra e usaram estimadores diferentes. Os resultados estão na tabela abaixo:Voc
Considere o CD-Notas e retire uma amostra com reposição de tamanho n = 10. Determine o erro padrão estimado pelo método bootstrap das estatísticas (use B = 15, por exemplo):(a) md = mediana da amostra
EMV na uniforme.
Suponha que X tenha distribuição N ( 0 ,0,09 ) . Uma amostra de tamanho 25 é obtida de X, digamos X1,...,X25. Qual é a probabilidade de que ∑ X i ² ²exceda 1,5?