Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 6º - Capítulo 11.Problemas - Ex. 42
EMV na uniforme.
Passo 1
Como:
A densidade conjunta da amostra é:
Segue-se que e derivando e igualando a zero obteremos , ou seja, o EMV de seria ! Evidentemente, essa não é a resposta. Na realidade, não podemos simplesmente derivar a verossimilhança (ou o logaritmo dela) para obter o máximo, pois temos as restrições para todo Façamos o seguinte. Considere o gráfico da densidade conjunta, ou da verossimilhança, como função de . Como devemos ter para todo, o máximo dos deve ser tal que , ou seja, obtemos o gráfico abaixo.
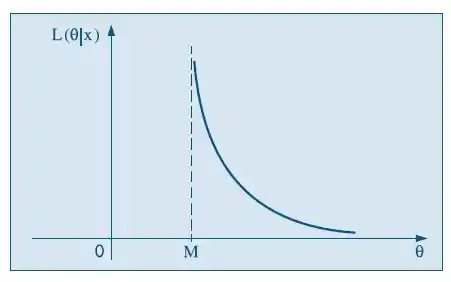
Ou seja, , para logo, o máximo da verossimilhança é obtido para e, portanto
Esse exemplo mostra que nem sempre obteremos o EMV derivando-se a verossimilhança e igualando-a a zero.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere uma amostra aleatória X 1 , X 2 , … , X n da fdp exponencial deslocada f ( x ; λ , θ ) = λ e - λ ( x - θ ) x ≥ θ 0 casocontrário á Considerando θ = 0 fornece a fdp da distribuição exponencia
No tempo t = 0 ; 20 componentes idênticos são examinados. A distribuição da vida útil de cada um é exponencial com parâmetro λ . O investigador deixa a instalação de teste sem monitoramento. Retornand
No tempo t = 0 , há um indivíduo com vida em certa população. Um processo de nascimento puro, então, desenvolve-se como segue. O tempo até o primeiro nascimento é exponencialmente distribuído com parâ
Quando a distribuição da população é normal, a mediana estatística X 1 - X ˜ , … , X n - X ˜ / 0,6745 é usada para estimar σ . O estimador é mais resistente aos efeitos de outliers (observações distan
Quando o desvio padrão da amostra S se baseia em uma amostra aleatória de uma distribuição normal da população, pode ser demonstrado que E ( S ) = 2 / ( n - 1 ) Γ ( n / 2 ) σ / Γ ( ( n - 1 ) / 2 ) Use