Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 3.Problemas - Ex. 36

Usando os dados da variável qualitativa região de procedência, da Tabela 2.1 , transforme-a na variável quantitativa X , definida do seguinte modo:

X = 1 ,   s e   a   r e g i ã o   d e   p r o c e d ê n c i a   f o r   c a p i t a l ; 0 ,   s e   a   r e g i ã o   d e   p r o c e d ê n c i a   f o r   i n t e r i o r   o u   o u t r a .

( a ) Calcule x - e v a r ( X ) .

( b ) Qual a interpretação de x - ?

( c ) Construa um histograma para X .

Passo 1

Bom galera, vamos começar calculando a média e a variância, primeiro a média:

x - = 11 36 = 0,305

E ao calcularmos a variância também encontraremos:

v a r X = 0,305

Passo 2

Belezinha, então se a gente pensar, de certa forma o valor da média indica a proporção de empregados que são da capital.

Pra terminar, nós fazemos um histograma:

Resposta

a   x - = 0,305 ; v a r X = 0,305

b   x -   é   a   p r o p o r ç ã o   d e   e m p r e g r a d o s   d a   c a p i t a l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Construa uma distribuição de frequências e um histograma para os dados do teor de algodão do exercício 6.16.
Construa uma distribuição de frequências em um histograma para os dados de octanagem do combustível para motor no exercício 6.14. Use oito intervalos de classe.
Construa uma distribuição de frequências e um histograma usando os dados de fratura do exercício 6.15
Construa uma distribuição de frequências e um histograma para os dados de rendimentos do exercício 6.17.
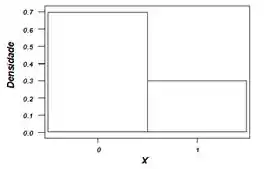
Construa uma distribuição de frequências histogramas, com 8 e 16 intervalos de classe para os dados de octanagem do combustível para motor do exercício 6.14. Compare os histogramas. Os dois histograma