Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 3.Problemas - Ex. 37
No Problema , do Capítulo , temos os resultados de funcionários em vários exames a que se submeteram. Sabe-se agora que os critérios adotados em cada exame não são comparáveis, por isso decidiu-se usar o desempenho relativo em cada exame. Essa medida será obtida do seguinte modo:
Para cada exame serão calculados a média e o desvio padrão .
A nota de cada aluno será padronizada do seguinte modo:
Interprete o significado de .
Calcule as notas padronizadas dos funcionários para o exame de Estatística.
Com os resultados obtidos em , calcule e .
Se alguma das notas padronizadas estiver acima de ou abaixo de , esse funcionário deve ser considerado um caso atípico. Existe algum nessa situação?
O funcionário obteve em Direito, em Estatística e em Política. Em que disciplina o seu desempenho relativo foi melhor?
Passo 1
Bom galera, se a gente pensar bem a gente nota que o valor de é uma nota padronizada, onde a média é indicada por . Dessa forma, mostra o desempenho em relação ao grupo.
Passo 2
Belezinha, se a gente calcular , as notas padronizadas são:
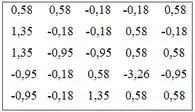
Como as notas foram padronizadas subtraindo a média e dividido pelo desvio padrão, temos que a média , enquanto que o desvio padrão .
Passo 3
Show de bola, como , então , então temos um caso atípico, pois temos uma nota que é .
E para avaliarmos o desempenho relativo, nós temos que comparar as notas padronizadas nas três disciplinas. Em direito todos tiveram , assim o funcionário teve a nota média, onde . Em politica a média das notas é , e o desvio padrão . Assim, a nota padronizada do funcionário é . Com isso, o desempenho relativo foi melhor em Política.
Resposta
;