Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 4.Problemas - Ex. 8

Qual o valor de χ 2 e de C para os dados do Problema 3? E para o Problema 6? Calcule T .

Passo 1

Primeiro, para revolvermos esse problema, precisamos supor a existência de independência entre as variáveis.

Ok! Mas como fazer isso?

DIRETO AO PONTO: Construindo uma tabelinha, na qual as proporções marginais se repetem no interior dessa tabela.

Para os dados do Problema 3 tem-se a tabela a seguir. Entre parênteses, encontram-se os valores esperados em caso de independência das variáveis.

Cálculo das frequências esperadas e i :

e 11 = 8 × 20 40 = 4                     e 12 = 8 × 20 40 = 4                     e 21 = 32 × 20 40 = 16                     e 22 = 32 × 20 40 = 16

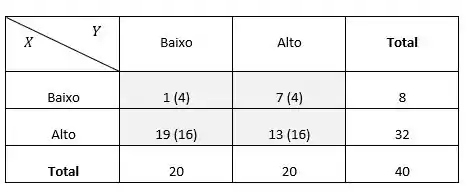
Calculando o qui-quadrado:

χ 2 = ∑ o i - e i 2 e i = 2,25 + 2,25 + 0,5625 + 0,5625 = 5,625

Calculando o Coeficiente de Contingência de Pearson:

C = χ 2 χ 2 + n = 5,625 5,525 + 40 = 0,351

Calculando o valor do coeficiente T :

T = χ 2 n r - 1 × s - 1 = 5,625 40 1 × 1 = 0,375

Passo 2

Já Para os dados do Problema 6 tem-se a tabela a seguir. Entre parênteses, encontram-se os valores esperados em caso de independência das variáveis.

Cálculo das frequências esperadas e i :

e 11 = 250 × 1000 2000 = 125                         e 12 = 250 × 1000 2000 = 125          

e 21 = 1750 × 1000 2000 = 875           e 22 = 1750 × 1000 2000 = 875

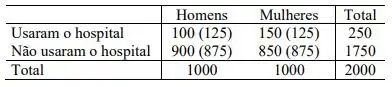
Calculando o qui-quadrado:

χ 2 = ∑ o i - e i 2 e i = 5,00 + 5,00 + 0,71 + 0,71 = 11,42

Calculando o Coeficiente de Contingência de Pearson:

C = χ 2 χ 2 + n = 11,42 11,42 + 2000 = 0,075

Calculando o valor do coeficiente T :

T = χ 2 n r - 1 × s - 1 = 11,42 2000 1 × 1 = 0,076

Resposta

Problema 3

χ 2 = 5,625

C = 0,351

T = 0,375

Problema 6

χ 2 = 11,42

C = 0,075

T = 0,076

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um exame vestibular para uma faculdade tem 80 questões, sendo 40 de português e40 de matemática. Para os 20 melhores classificados, apresentamos o número de acertos em cada disciplina, em ordem decres
Vinte baterias para automóveis de uma certa marca foram testadas quanto à sua vida útil. O teste simula a utilização da bateria, acelerando seu desgaste de modo a criar uma réplica da situação real. O
Deseja-se comparar três técnicas cirúrgicas para a extração de dente de siso. Cada uma das técnicas foi aplicada em 20 pacientes e os resultados são apresentados a seguir.d. Se você é otimista, qual t
Um exame vestibular para uma faculdade tem 80 questões, sendo 40 de português e40 de matemática. Para os 20 melhores classificados, apresentamos o número de acertos em cada disciplina, em ordem decres
Um exame vestibular para uma faculdade tem 80 questões, sendo 40 de português e40 de matemática. Para os 20 melhores classificados, apresentamos o número de acertos em cada disciplina, em ordem decres